Tag: Math
-

Robot Walks
—
by
I’ve gotten a lot of mathematical inspiration from Project Euler questions, but perhaps the question that has gotten me thinking the most is Project Euler Problem 208: Robot Walks. In this problem, a robot takes steps either to the right or the left, and at each step, it turns \(\frac 15\) of the way of…
-

Zimin Words and Bifixes
—
by
One of the earliest contributions to the On-Line Encyclopedia of Integer Sequences (OEIS) was a family sequences counting the number of words that begin (or don’t begin) with a palindrome: Let \(f_k(n)\) be the number of strings of length \(n\) over a \(k\)-letter alphabet that begin with a nontrivial palindrome” for various values of \(k\).…
-

My Favorite Sequences: A263135
—
by
This is the fourth in my installment of My Favorite Sequences. This post discusses sequence A263135 which counts penny-to-penny connections among \(n\) pennies on the vertices of a hexagonal grid. I published this sequence in October 2015 when I was thinking about hexagonal-grid analogs to the “Not Equal” grid. The square-grid analog of this sequence…
-

My Favorite Sequences: “Not Equal” Grid
—
by
This is the third installment in a recurring series, My Favorite Sequences. This post discusses OEIS sequence A278299, a sequence that took over two years to compute enough terms to add to the OEIS with confidence that it was distinct. This sequence is discussed in Problem #23 of my Open Problems Collection, which asks for…
-
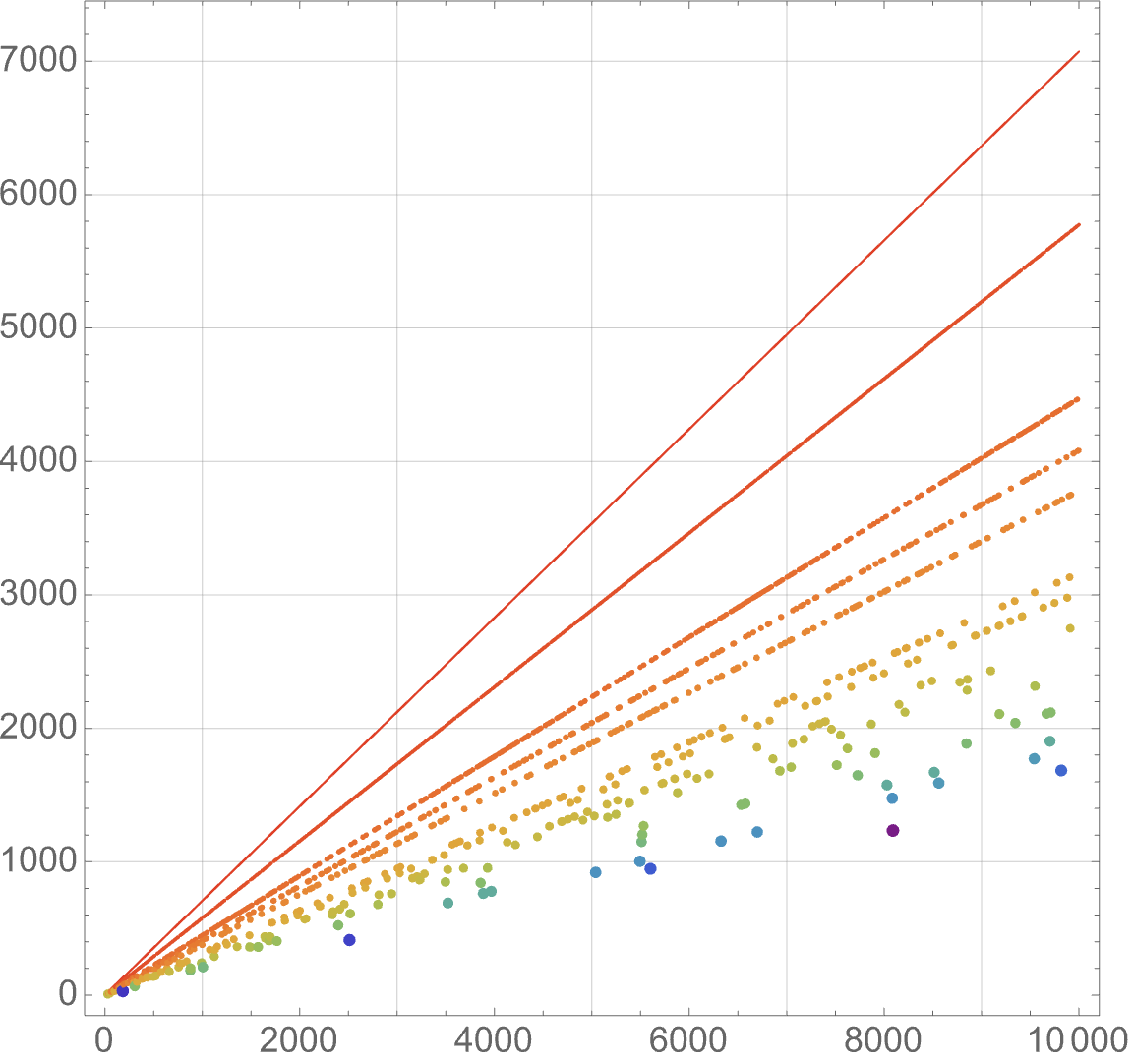
My Favorite Sequences: A261865
—
by
This is the first installment in a new series, “My Favorite Sequences”. In this series, I will write about sequences from the On-Line Encyclopedia of Integer Sequences that I’ve authored or spent a lot of time thinking about. I’ve been contributing to the On-Line Encyclopedia of Integer Sequences since I was an undergraduate. In December…
-
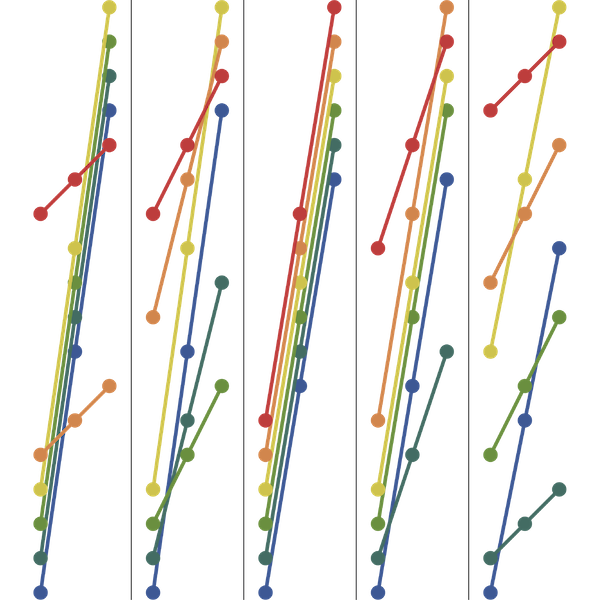
Richard Guy’s Partition Sequence
—
by
Neil Sloane is the founder of the On-Line Encyclopedia of Integer Sequences (OEIS). Every year or so, he gives a talk at Rutgers in which he discusses some of his favorite recent sequences. In 2017, he spent some time talking about a 1971 letter that he got from Richard Guy, and some questions that went…
-

A π-estimating Twitter bot: Part I
—
by
This is the first part of a three part series about making the Twitter bot @BotfonsNeedles. In this part, I will write a Python 3 program that uses a Monte Carlo method to approximate \(\pi\) with Buffon’s needle problem, and produces an image with the Python library Pillow In the second part, I’ll explain how…
-
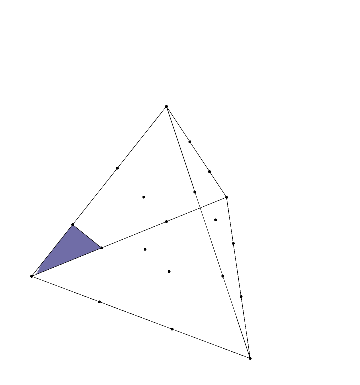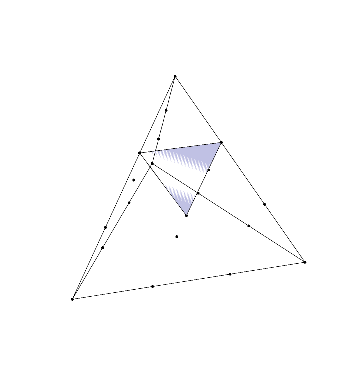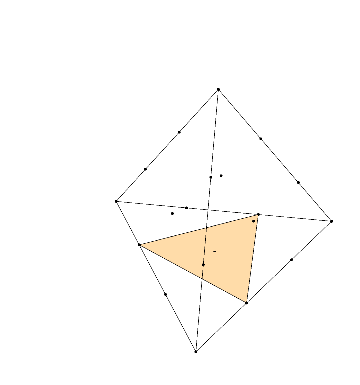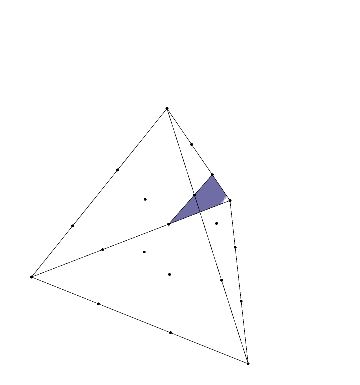
Polytopes with Lattice Coordinates
—
by
Problems 21, 66, and 116 in my Open Problem Collection concern polytopes with lattice coordinates—that is, polygons, polyhedra, or higher-dimensional analogs with vertices the square or triangular grids. (In higher dimensions, I’m most interested in the \(n\)-dimensional integer lattice and the \(n\)-simplex honeycomb). This was largely inspired by one of my favorite mathematical facts: given…
-

Stacking LEGO Bricks
—
by
Back in May, I participated in The Big Lock-Down Math-Off from The Aperiodical. In the Math-Off, I went head-to-head against Colin Beveridge (who has, hands-down, my favorite Twitter handle: @icecolbeveridge). Colin wrote about using generating functions to do combinatorics about Peter Rowlett’s toy Robot Caterpillar. Coincidentally and delightfully, I wrote about using generating functions to…
-
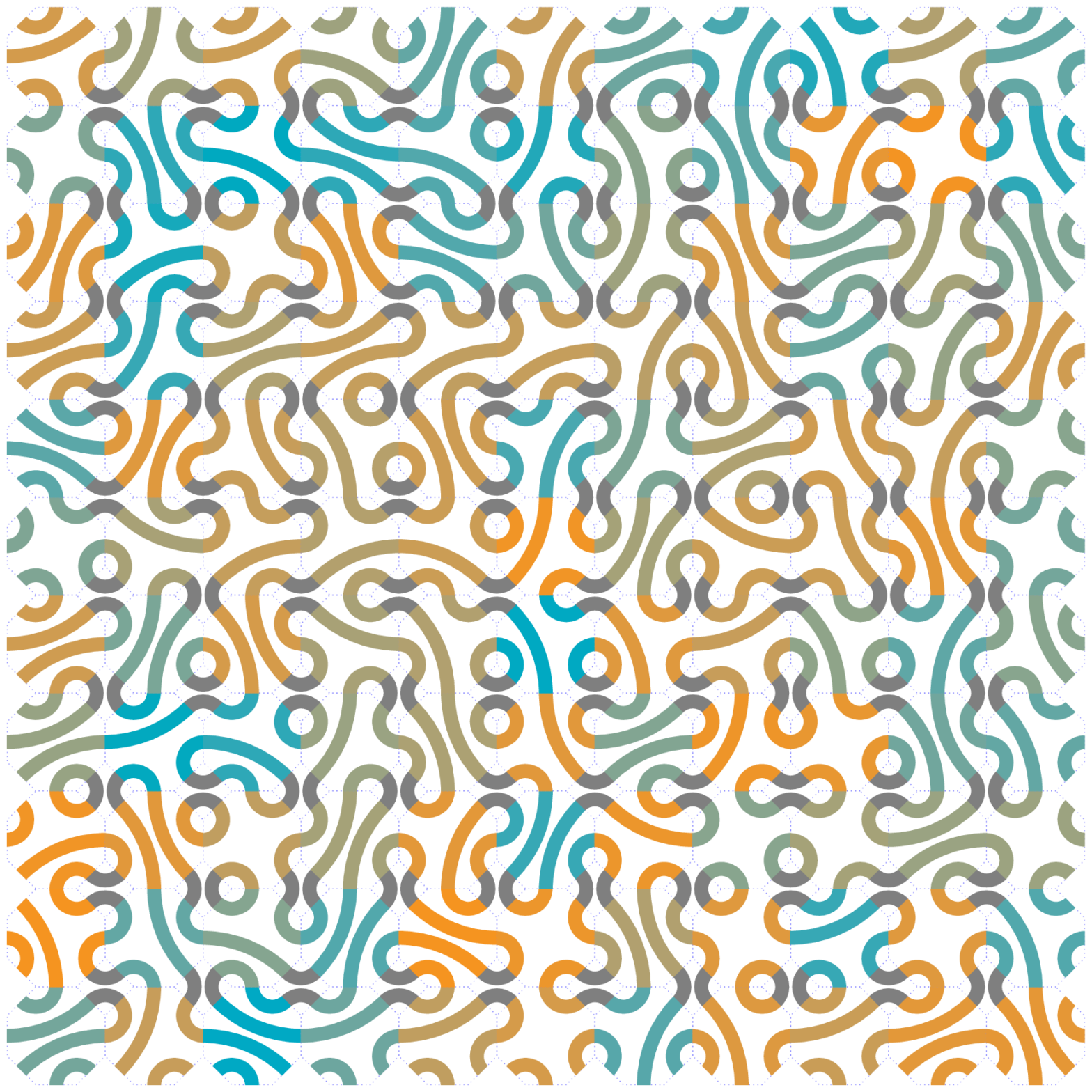
Regular Truchet Tilings
—
by
I recently made my first piece of math art for my apartment: a 30″×40″ canvas print based on putting Truchet tiles on the truncated trihexagonal tiling. I first became interested in these sorts of patterns after my former colleague Shane sent me a YouTube video of the one-line Commodore 64 BASIC program: 10 PRINT CHR$(205.5+RND(1));…