Neil Sloane is the founder of the On-Line Encyclopedia of Integer Sequences (OEIS). Every year or so, he gives a talk at Rutgers in which he discusses some of his favorite recent sequences. In 2017, he spent some time talking about a 1971 letter that he got from Richard Guy, and some questions that went along with it. In response to the talk, I investigated the letter and was able to sort out Richard’s 45-year-old idea, and correct and compute some more terms of his sequence.
Richard Guy and his sequences
Richard Guy was a remarkable mathematician who lived to the remarkable age of 103 years, 5 months, and 9 days! His life was filled with friendships and collaborations with many of the giants of recreational math: folks like John Conway, Paul Erdős, Martin Gardner, Donald Knuth, and Neil Sloane. But what I love most about Richard is how much joy and wonder he found in math. (Well, that and his life-long infatuation with his wife Louise.)
[I’m] an amateur [mathematician], I mean I’m not a professional mathematician. I’m an amateur in the more genuine sense of the word in that I love mathematics and I would like everybody in the world to like mathematics.
Richard Guy in Fascinating Mathematical People: Interviews and Memoirs
Richard’s letter to Neil
In January 2017, Neil Sloane gave a talk at Doron Zeilberger’s Experimental Mathematics Seminar, and about six minutes in, Neil discusses a letter that Richard sent to him at Cornell—which was the forwarded to Bell Labs—in June 1971.
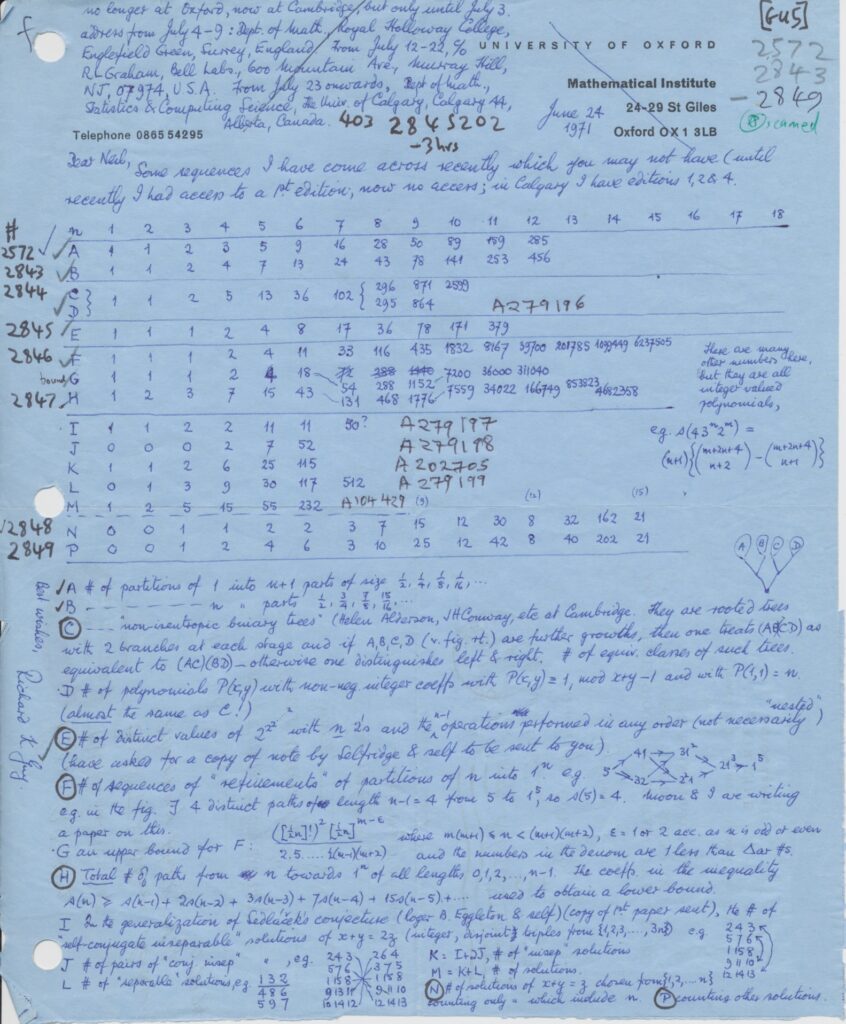
When I was working on the book, the 1973 Handbook of Integer Sequences, I would get letters from Richard Guy from all over the world. As he traveled around, he would collect sequences and send them to me.
Neil Sloane, Rutgers Experimental Mathematics Seminar
At 11:30, Neil discusses “sequence I” from Richard’s letter, which he added to the OEIS as sequence A279197:
Number of self-conjugate inseparable solutions of \(X + Y = 2Z\) (integer, disjoint triples from \(\{1,2,3,\dots,3n\}\)).
Neil mentioned in the seminar that he didn’t really know exactly what the definition meant. With some sleuthing and programming, I was able to make sense of the definition, write a Haskell program, correct the 7th term, and extend the sequence by a bit. The solutions for \(A279197(1)\) through \(A279197(10)\) are listed in a file I uploaded to the OEIS, and Fausto A. C. Cariboni was able to extend the sequence even further, submitting terms \(A279197(11)\)–\(A279197(17)\).
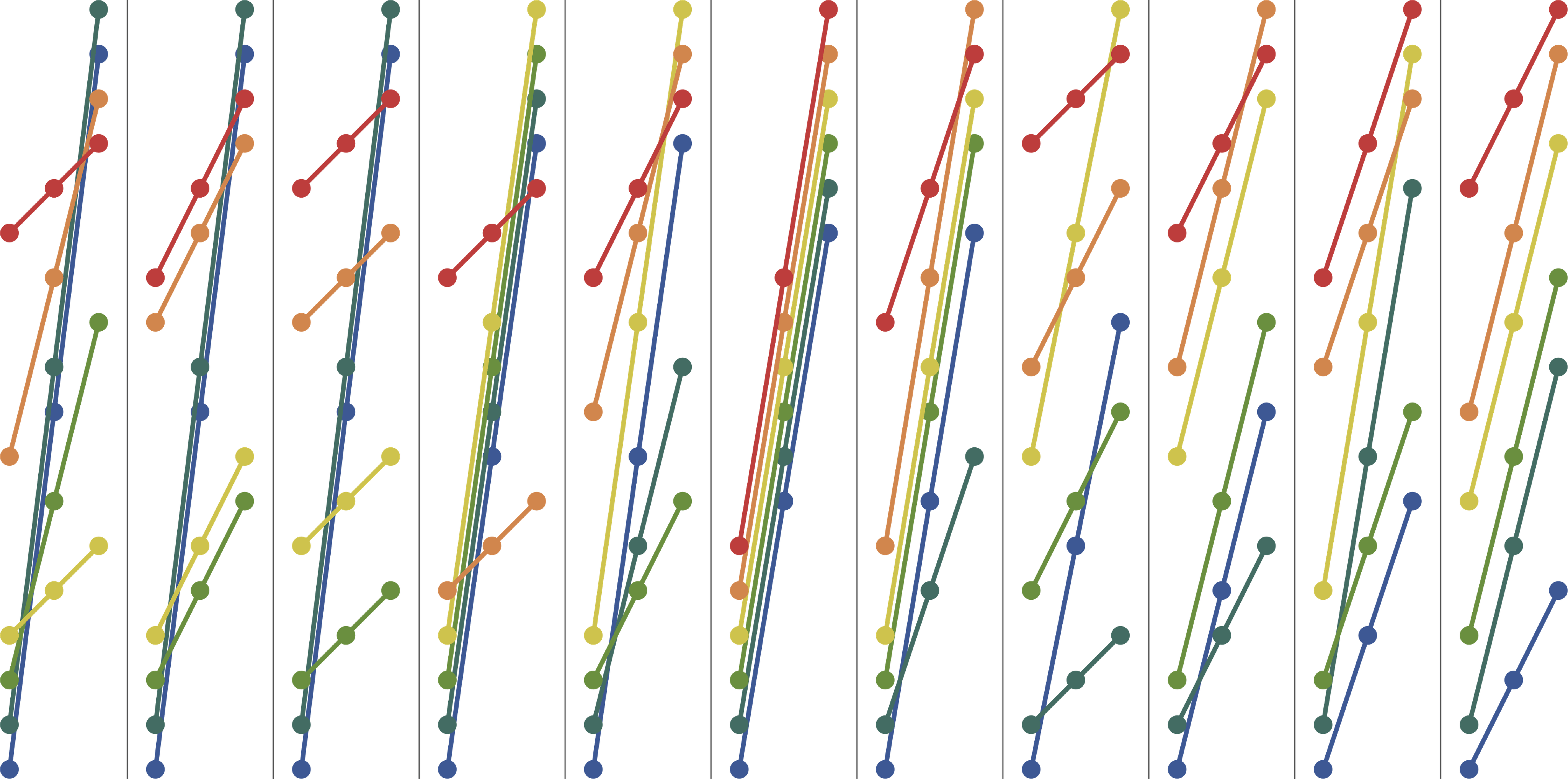
How the sequence works.
The idea here is to partition \(\{1,2,3,\dots,3n\}\) into length-3 arithmetic progressions, \(\bigl\{\{X_i,Z_i,Y_i\}\bigr\}_{i=1}^{n}\). And in particular, we want them to be inseparable and self-conjugate.
An inseparable partition is one whose “smallest” subsets are not a solution for a smaller case. For example, if \(n=3\), then the partition \[\bigl\{ \{1,3,5\}, \{2,4,6\}, \{7,8,9\} \bigr\}\] is separable, because if the subset \(\bigl\{ \{1,3,5\}, \{2,4,6\} \bigr\}\) is a solution to the \(n=2\) case.
A self-conjugate partition is one in which swapping each \(i\) with each \(3n+1-i\) gets back to what we started with. For example, \(\bigl\{\{1,3,5\}, \{2,4,6\}\bigr\}\) is self-congugate, because if we replace the \(1\) with a \(6\) and the \(2\) with a \(5\), and the \(i\) with a \(7-i\), then we get the same set: \(\bigl\{\{6,4,2\}, \{5,3,1\} \bigr\}\)
(1,3,5), (2,7,12), (4,9,14), (6,8,10), (11,13,15) (1,3,5), (2,8,14), (4,7,10), (6,9,12), (11,13,15) (1,5,9), (2,3,4), (6,8,10), (7,11,15), (12,13,14) (1,5,9), (2,4,6), (3,8,13), (7,11,15), (10,12,14) (1,6,11), (2,3,4), (5,10,15), (7,8,9), (12,13,14) (1,6,11), (2,7,12), (3,8,13), (4,9,14), (5,10,15) (1,7,13), (2,4,6), (3,9,15), (5,8,11), (10,12,14) (1,7,13), (2,8,14), (3,9,15), (4,5,6), (10,11,12) (1,8,15), (2,3,4), (5,6,7), (9,10,11), (12,13,14) (1,8,15), (2,4,6), (3,5,7), (9,11,13), (10,12,14) (1,8,15), (2,4,6), (3,7,11), (5,9,13), (10,12,14)
Generalizing Richard Guy’s idea
Of course, it’s natural to wonder about the separable solutions, or what happens if the self-conjugate restriction is dropped. In exploring these cases, I found four cases already in the OEIS, and I computed five more: A282615–A282619.
| Separable | Inseparable | Either | |
| Self-conjugate | A282615 | A279197 | A282616 |
| Non-self-conjugate | A282618 | A282617 | A282619 |
| Either | A279199 | A202705 | A104429 |
Generalizing further
There are lots of other generalizations that might be interesting to explore. Here’s a quick list:
- Look at partitions of \(\{1,2,\dots,kn\}\) into \(n\) parts, all of which are an arithmetic sequence of length \(k\).
- Count partitions of \(\{1,2,\dots,n\}\) into any number of parts of (un)equal size in a way that is (non-)self-conjugate and/or (in)separable.
- Consider at partitions of \(\{1,2,\dots,3n\}\) into \(n\) parts, all of which are an arithmetic sequence of length \(3\), and whose diagram is “non-crossing”, that is, none of the line segments overlap anywhere. (See the 6th and 11th cases in the example for \(A279197(6) = 11\).)
If explore any generalizations of this problem on your own, if you’d like to explore together, or if you have an anecdotes about Richard Guy that you’d like to share, let me know on Twitter!
Leave a Reply