Blog
-
Nerd sniped by Richard Stanley
I got nerd sniped by this first open problem described in a MathOverflow post by Richard Stanley, which suggests that there’s good reason to suspect that an innocuous-seeming combinatorial function might grows faster than any recursive function!
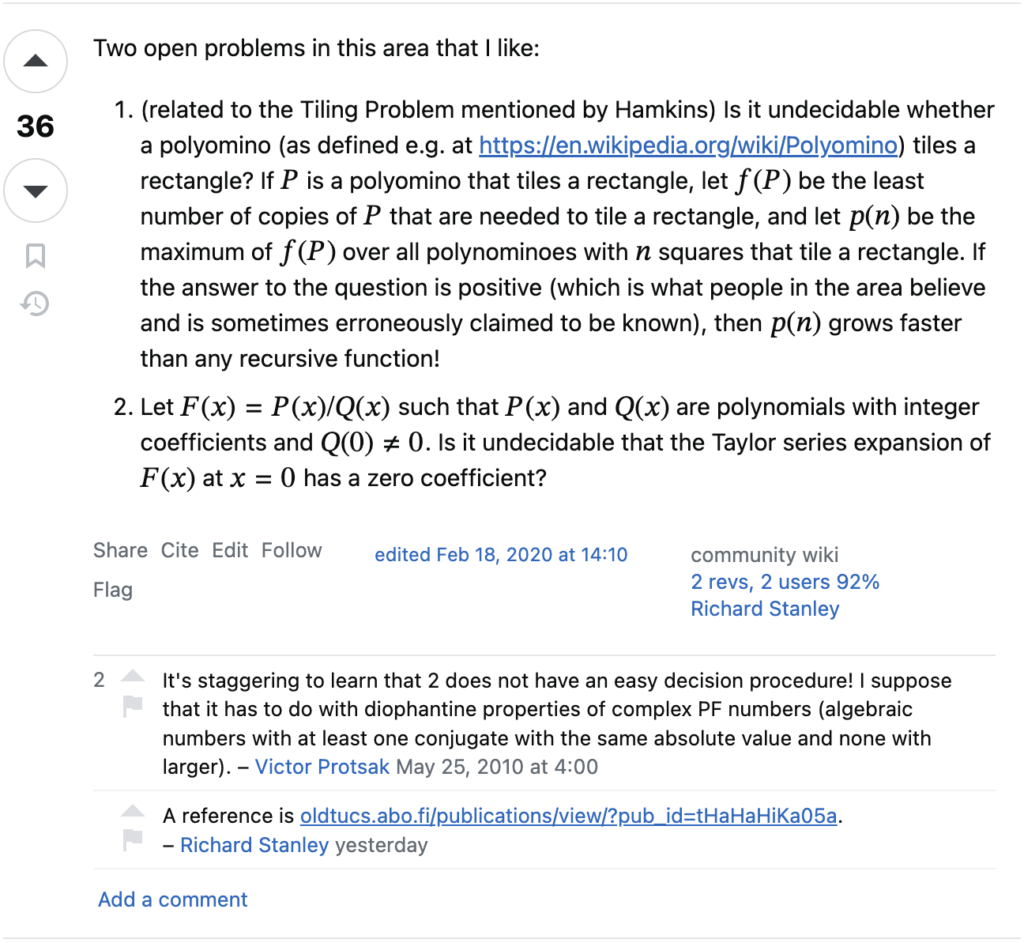
This sounds right up my alley, but I when I read this, I didn’t have any intuition for how to think about \(f(P)\) and \(p(n)\), so I wrote this post to investigate it for myself and share that with you. (After all, I tell my students: “writing is thinking.”)
My first step was to write down some examples and search for the \(p\)-sequence in the OEIS. (After all, I tell my students: “start by writing down some examples.”)
Intuition from examples
- (\(n=1\) and \(n=2\)) There’s only one \(1\)-omino, the square, and only one \(2\)-omino, the domino. Since both are rectangles, \(p(1) = p(2) = 1\).
- (\(n=3\)) There are two \(3\)-ominos:
- We can tile a rectangle with one copy of
 .
. - We can tile a rectangle with two copies of
 .
. - Therefore \(p(3) = 2\).
- We can tile a rectangle with one copy of
- (\(n=4\)) There are five free \(3\)-ominos:
- We can tile a rectangle with 1 copy of
 .
. - We can tile a rectangle with 1 copy of
 .
. - We can tile a rectangle with 2 copies of
 .
. - We can tile a rectangle with 4 copies of
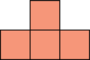 .
. - We cannot tile a rectangle with any number of copies of
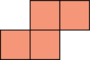 .
. - Therefore \(p(4) = 4\).
- We can tile a rectangle with 1 copy of
OEIS sequence A126140
I found OEIS sequence A126140 by searching for
1, 1, 2, 4 polyomino rectangle.
Rectifiable polyominoes
The OEIS sequence led me to Michael Reid’s website, which led me to a host of resources studying these objects. Here’s a definition of rectifiable polyominoes and their orders that matches Richard Stanley’s definition.
- A polyomino is said to be rectifiable if a certain number of copies of the polyomino will together form a rectangle.
- The order of a polyomino is the smallest number of pieces needed to form a rectangle.
Rectangular tilings
The following examples come from Michael Reid’s data on rectifiable polyominoes and WaybackMachine archive of Erich Friedman’s list of “Polyominoes in Rectangles.” Take a look at those links for more examples and background.
\(\operatorname{A126140}(5) = p(5) = 10\)
The largest minimal rectangle of a \(5\)-omino is a \(10\times5\) packing:
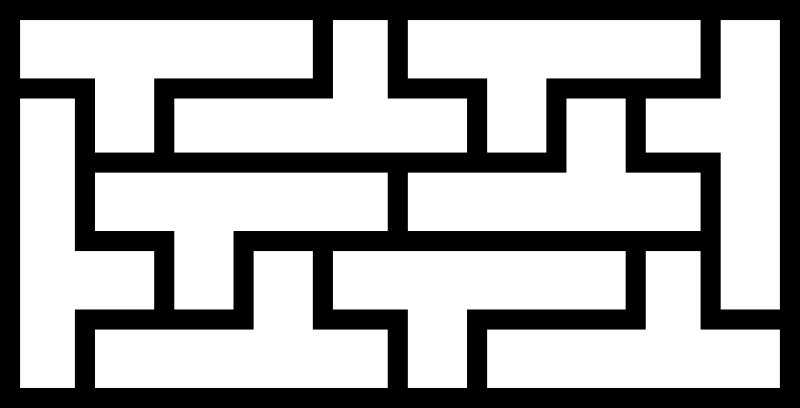
The first published example of this that I could find was by David A. Klarner in “Some results concerning polyominoes” in the Fibonacci Quarterly (1965).
\(\operatorname{A126140}(6) = p(6) = 92\)
The largest minimal rectangle of a \(6\)-omino is a \(24\times23\) packing, which was first found by T.W. Marlow and published in Chessics #23 (1985), “the journal of generalized chess,” and then seems to have been independently discovered and published by Karl A Dahlke as “The Y-hexomino has order 92” in (the quite presigious) Journal of Combinatorial Theory, Series A.


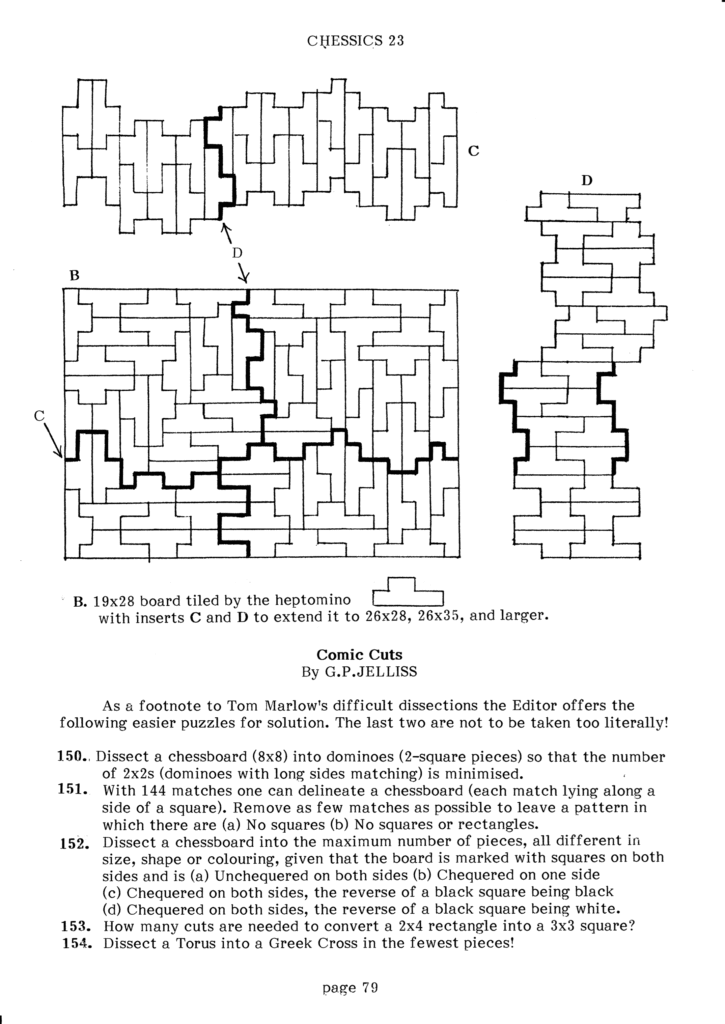
\(\operatorname{A126140}(7) = p(7)=76\)
The largest minimal rectangle of a \(7\)-omino is a \(19\times28\) packing:

This was first published by Karl A. Dahlke in JCTA in the 1989 article “A Heptomino of Order 76.”
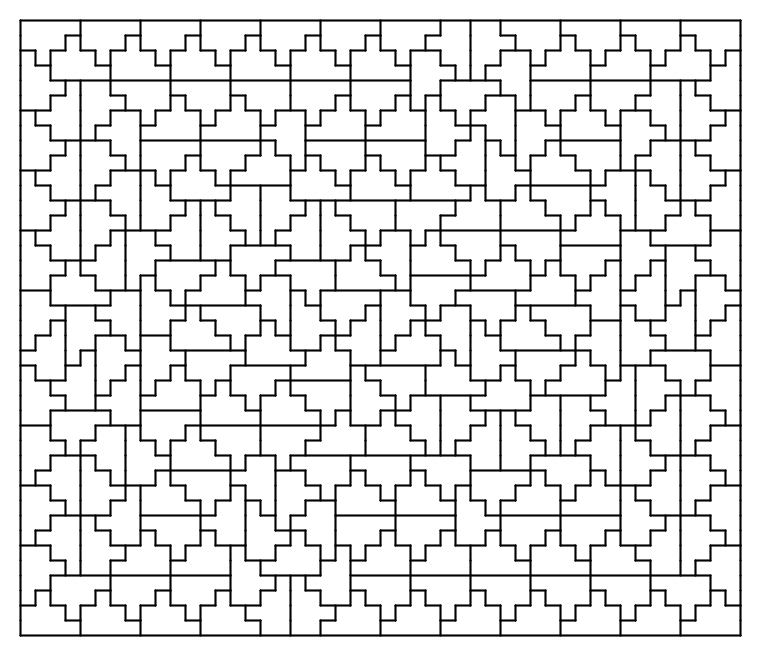
\(\operatorname{A126140}(8) = p(8)=246\)
The largest minimal rectangle of a \(8\)-omino is a \(41\times48\) packing. It looks like Karl Dahlke computes this and has the code on Github as “trec.”
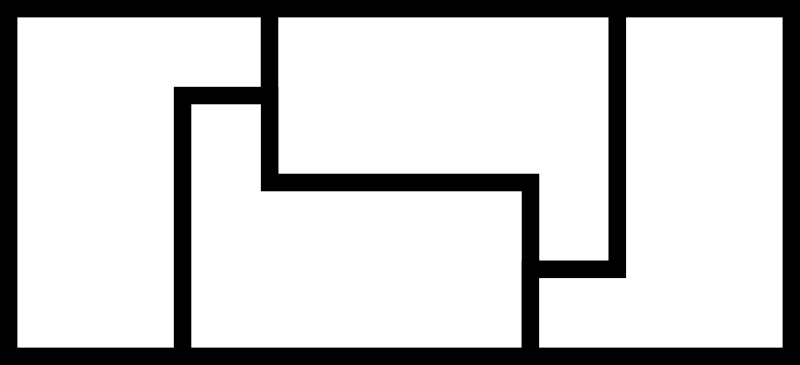
\(\operatorname{A126140}(9) = p(9)=4\)
The largest minimal rectangle of a \(9\)-omino is \(6\times6\) or \(9\times4\). Many \(9\)-ominos have \(f(P) = 4\), but the \(9\times4\) rectangle seems to occur only for one \(9\)-omino.
Other “prime”
Michael Reid’s data gives larger polyominos with “prime” rectangles, those which do not contain any smaller rectangle. However, it’s not clear if these rectangles are claimed to be minimal (in which case, for example, \(p(10) \geq 138\)) or if all polyominoes have been checked. Nevertheless the packings are all visually interesting, so I’ve copied them here.
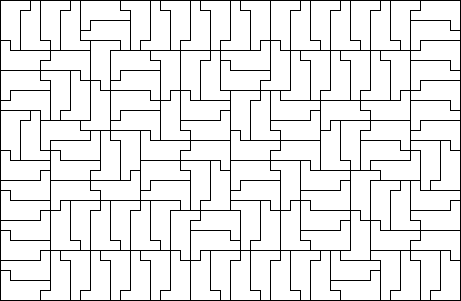
10-omino (30 × 46) 
11-omino (54 × 55) 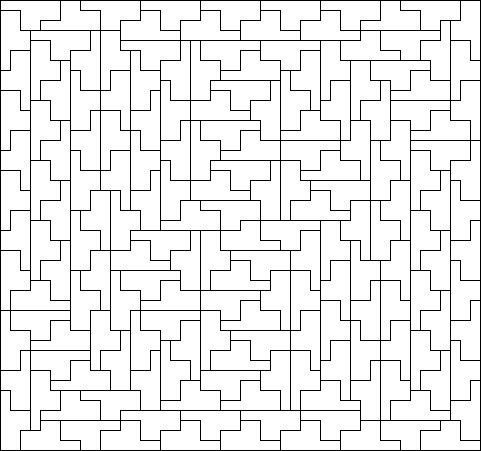
12-omino (45 × 48) 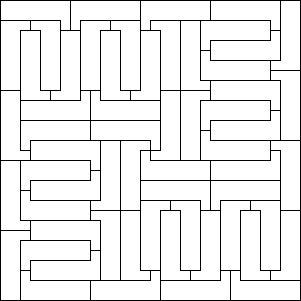
15-omino (30 × 30) Bluesky
Want to chat more about this! Let me know on Bluesky!
-
Straightedge and Compass Constructions (2 of 2)
This post contains images based on the straightedge-and-compass constructions discussed in Part 1.
Plotting points

All of the \(5743\) points that can be drawn using five or fewer lines/circles in a straightedge-and-ruler construction, starting with just the initial points of \((0,0)\) and \((1,0)\). 
All of the \(1704\) points that can be drawn using five or fewer circles (and no lines) in a straightedge-and-ruler construction, starting with just the initial points of \((0,0)\) and \((1,0)\). All the circles and lines
Just for fun, here are two other images, the first shows all of the distinct lines and circles you can draw using a ruler-and-compass in at most five steps. The second show all of the distinct circles you can draw within five steps using just a compass.

The 1337 circles and 596 lines that appear in a ≤5-step construction. 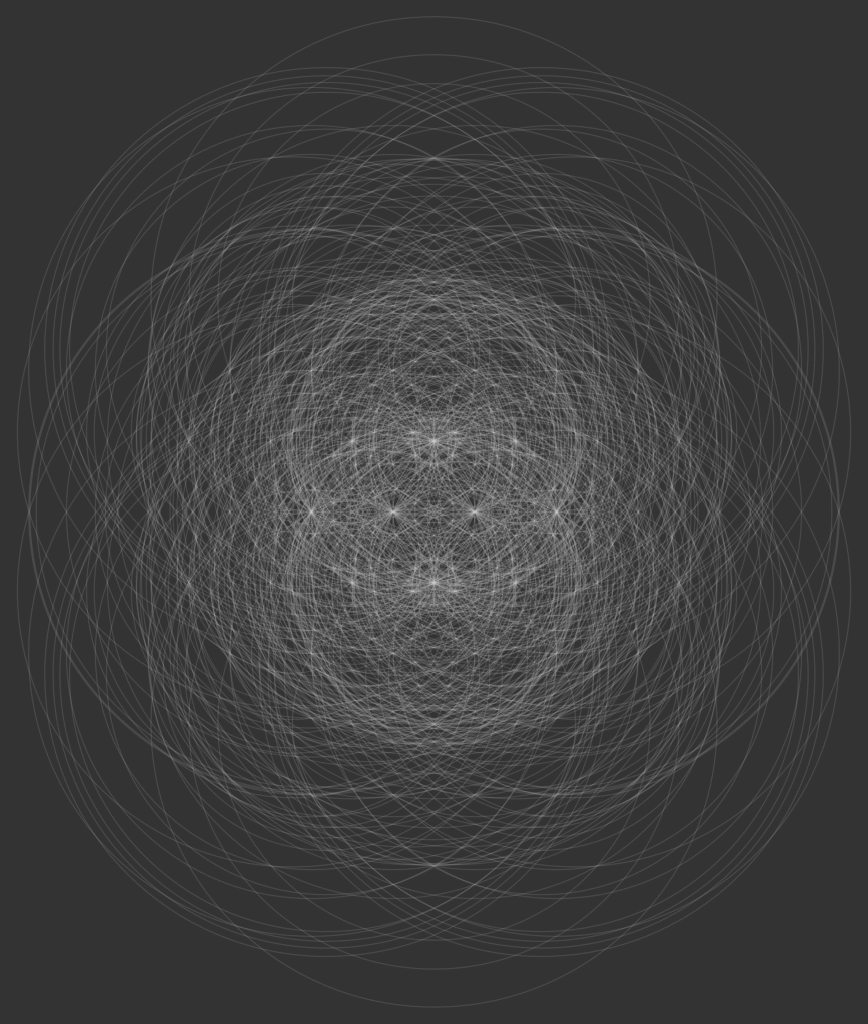
The 480 circles that appear in a ≤5-step compass-only construction. -
Straightedge and Compass Constructions (1 of 2)
How many distinct constructions can be made with a straightedge and compass if we draw \(n\) lines and circles?
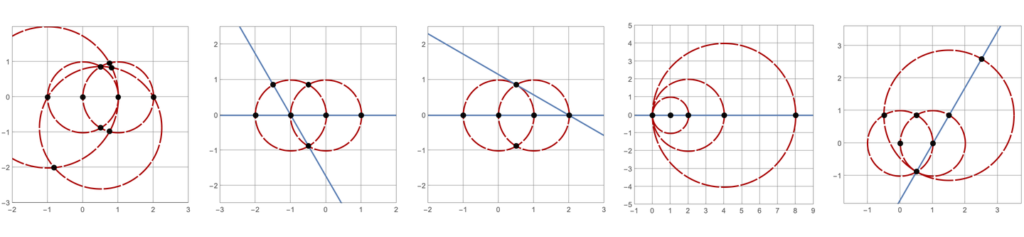
An example of five straightedge-and-compass constructions each with \(5\) lines and circles. Describing a straightedge-and-compass construction
Initially we start with two points, which we call \((0,0)\) and \((1,0)\). At each step, we can do one of two things:
- Straightedge. We can use the straightedge to draw the line connecting any two points.
- Compass. We can place the needle of a compass at a point \(p_1\), and the other tip at another point \(p_2\), and draw the circle centered at \(p_1\) that goes through \(p_2\)
We get new points whenever lines intersect with lines, lines intersect with circles, or circles intersect with circles.
The On-Line Encyclopedia of Integer Sequences (OEIS)
I’ve added this to the OEIS as sequence A383082, which begins $$1, 3, 3, 16, 205, 5886, 542983, \dots.$$ I’ve illustrated some of the terms of this sequence here.
There’s a theorem, the Mohr–Mascheroni theorem, which states that any points that can be constructed with a straightedge and compass, can be constructed with a compass alone. This is the motivation for OEIS as sequence A383083, which gives the number of constructions with \(n\) circles and no lines and begins $$1, 2, 1, 4, 44, 1084, 91192, \dots.$$
\(A383082(1) = 3\)
Here are the three constructions with one line or circle.
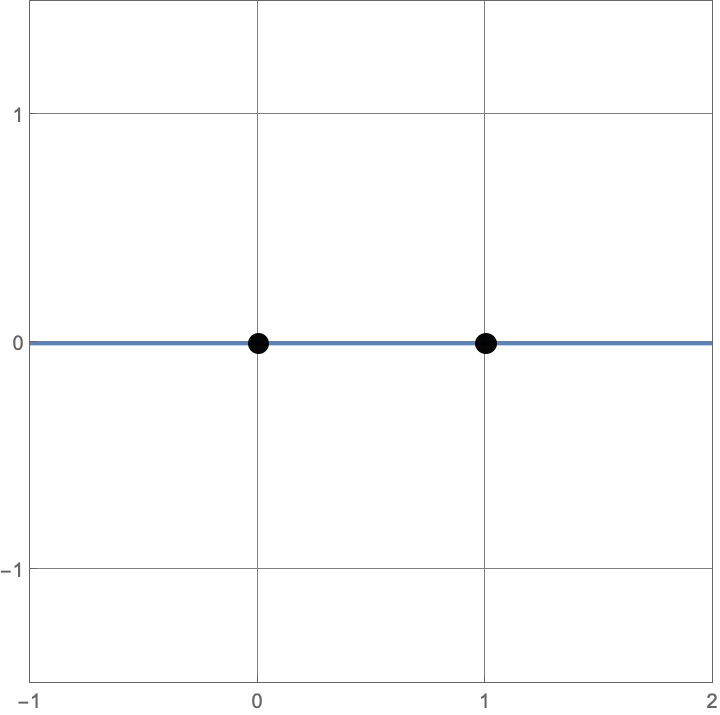
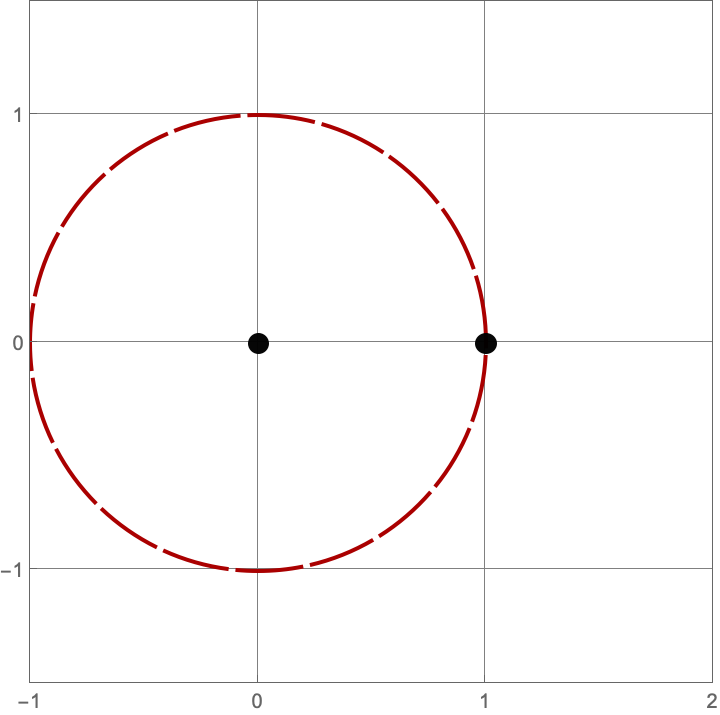
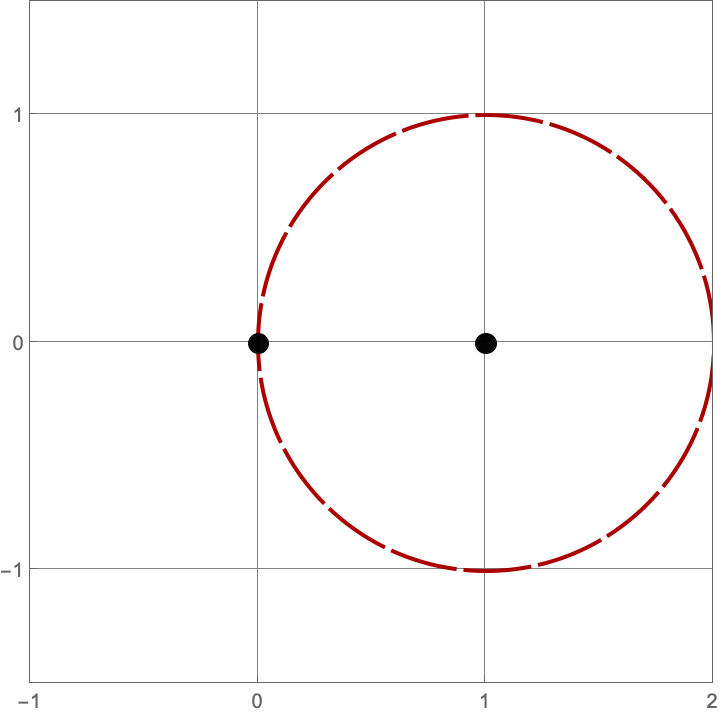
\(A383082(2) = 3\)
Here are the three constructions with two lines and circles.

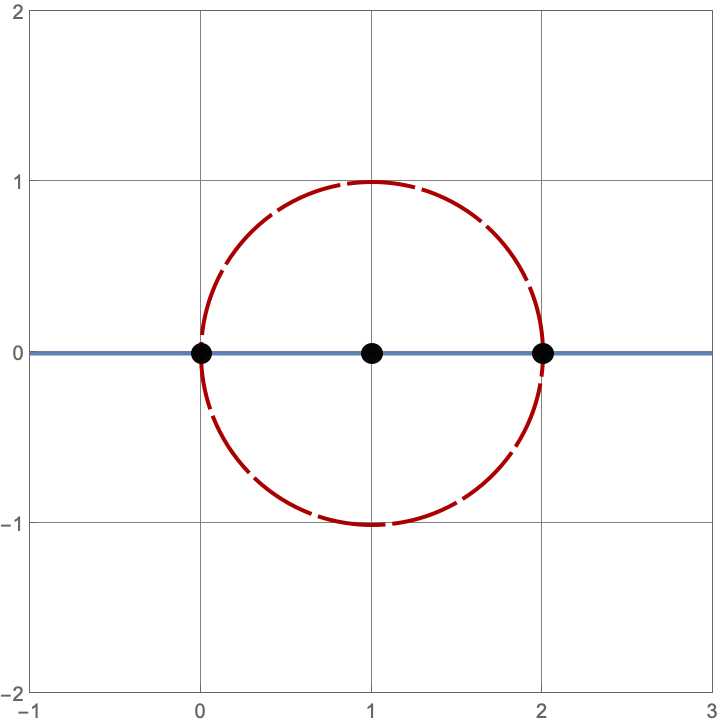
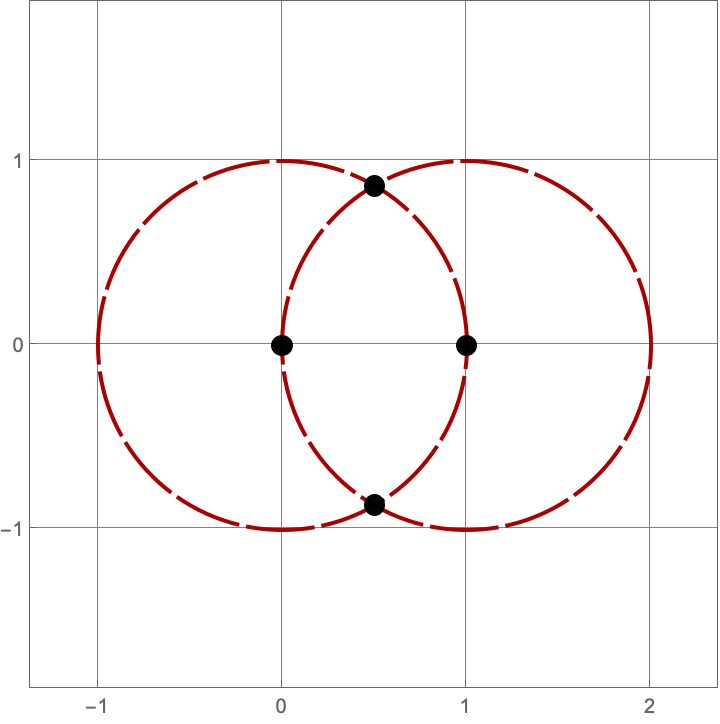
\(A383082(3) = 16\)
Here are the sixteen constructions with three lines and circles.
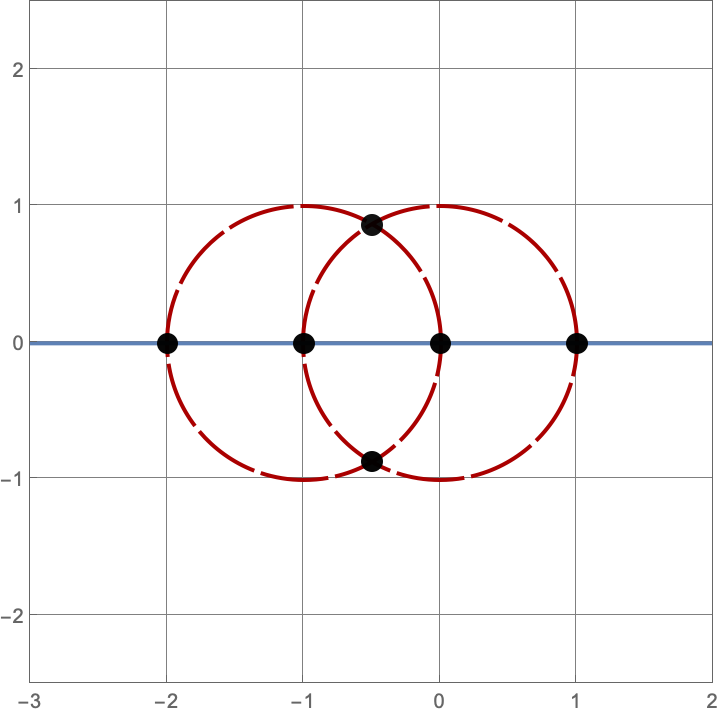
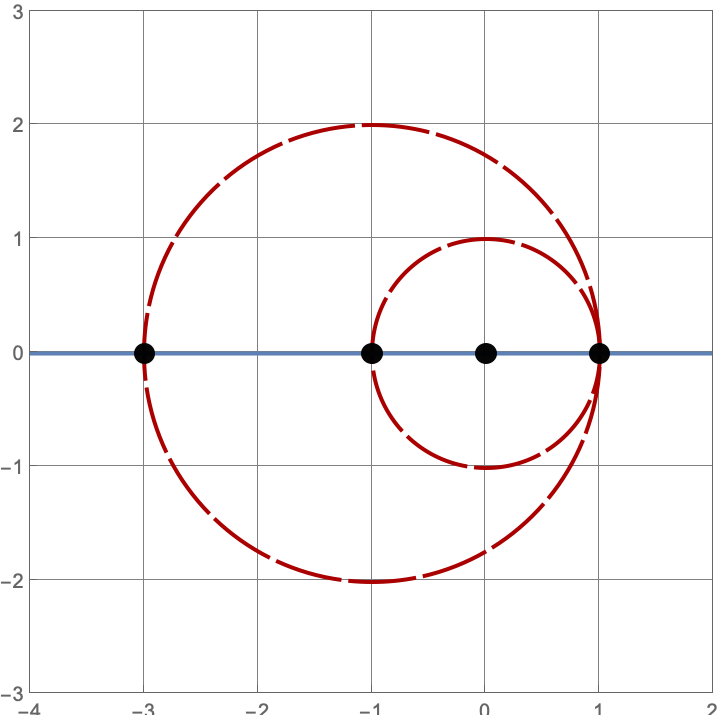
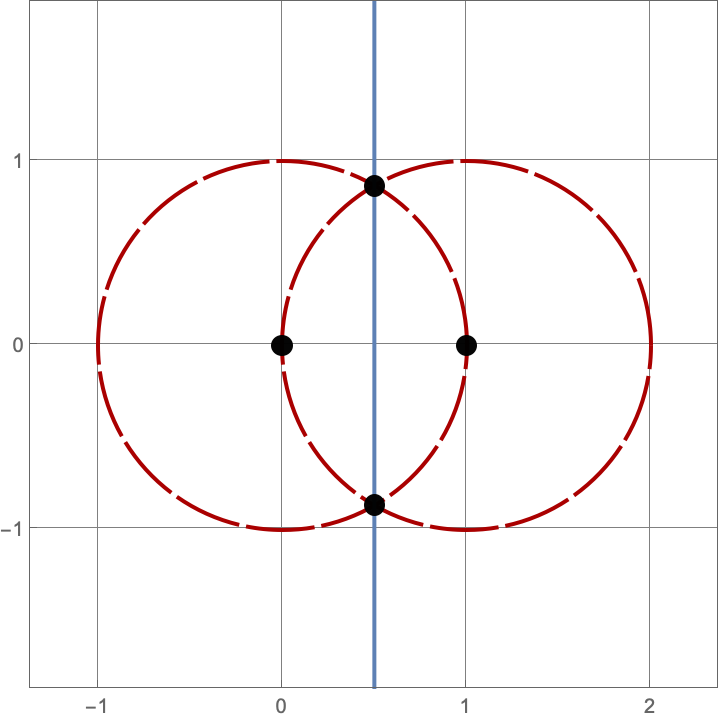
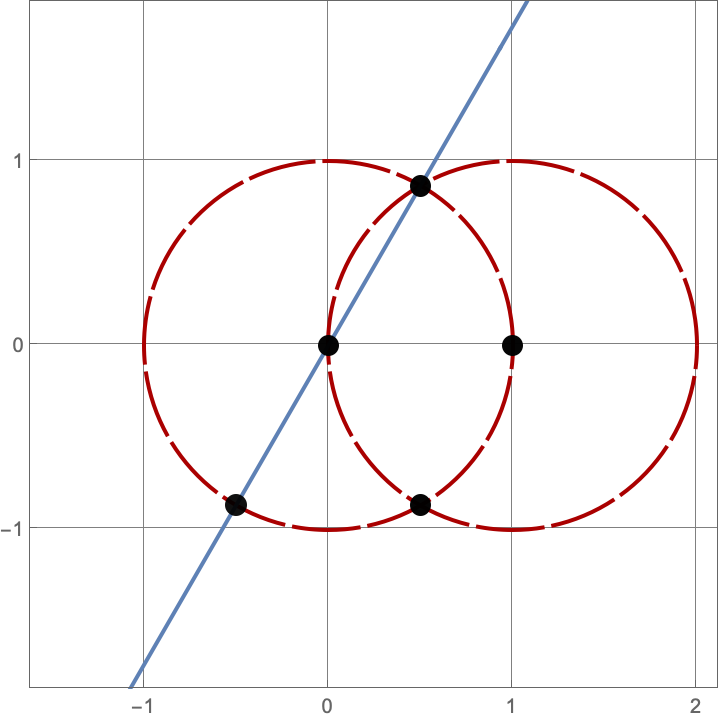
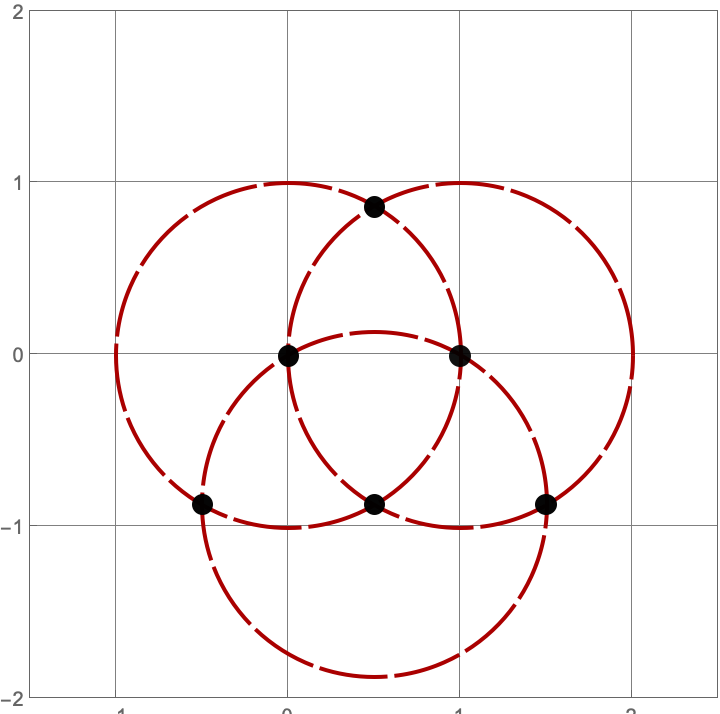
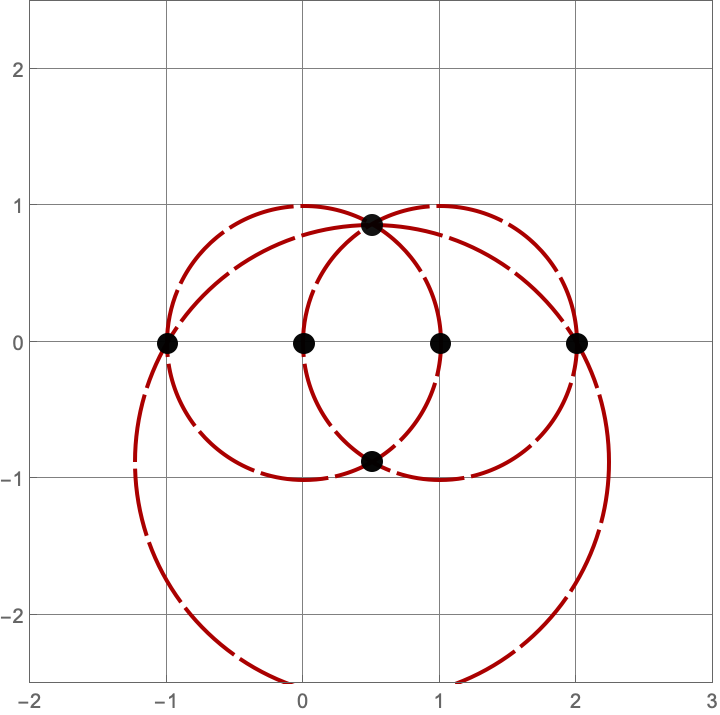
\(A383082(4) = 205\)
There are \(\operatorname{A383082}(4) = 205\) constructions with \(4\) lines and circles. Here’s a sample of five such constructions. Click on the image to see all \(205\) of them.

\(n\le5\)
Watch the video below to see all \(1 + 3 + 3 + 16 + 205 + 5886 = 6114\) constructions with \(5\) or fewer lines and circles played at 60 fps for 1.7 minutes.
Computing the sequences
In total, I computed six sequence, which I submitted to the OEIS:
- A383082: The number of distinct straightedge-and-ruler constructions that can be made with a total of \(n\) lines and circles. $$1, 3, 3, 16, 205, 5886, 542983$$
- A383083: The number of distinct straightedge-and-compass constructions that can be made with no lines and \(n\) circles.$$1, 2, 1, 4, 44, 1084, 91192$$
- A383084: The number of points in the Euclidean plane that can be determined via a straightedge-and-compass construction using \(n\) or fewer lines and circles. $$2, 2, 6, 14, 147, 5743$$
- A383085: The number of points in the Euclidean plane that can be determined via a straightedge-and-compass construction using no lines and \(n\) or fewer circles. $$2, 2, 4, 10, 52, 1704, 214135$$
- A383086: The number of distinct distances between points in the Euclidean plane where the points are constructed via a straightedge-and-compass construction using \(n\) lines and no circles. $$1, 1, 2, 4, 35, 2480$$
- A383087: The number of distinct distances between points in the Euclidean plane where the points are constructed via a straightedge-and-compass construction using \(n\) lines and circles. $$1, 1, 3, 5, 73, 6628$$
(I’m most optimistic about being able to extend A383084. I’m least optimistic about being able to extend A383083.)
Haskell code
I computed the sequence originally in Mathematica and then checked my work in Haskell using Anders Kaseorg’s library Constructible. Here’s the Haskell code that I used to compute the OEIS sequences.
module Helpers.RulerAndCompass (rulerAndCompassConstructions, compassConstructions, distinctDistances) where import Data.Real.Constructible (Construct) import Data.Set (Set) import qualified Data.Set as Set import Data.List (tails) import Helpers.SetHelpers (flatMap) type Diagram = (Set Point, Set Curve) type Point = (Construct, Construct) data Curve = VerticalLine Construct -- x_0 | GeneralLine Construct Construct -- m & b for | Circle Point Construct deriving (Show, Eq, Ord) lineFromPoints :: (Point, Point) -> Curve lineFromPoints ((x1,y1), (x2,y2)) = if x1 == x2 then VerticalLine x1 else GeneralLine m b where m = (y2-y1)/(x2-x1) b = (x2*y1 - x1*y2)/(x2-x1) dist (x1,y1) (x2,y2) = sqrt ((x2 - x1)^2 + (y2 - y1)^2) circlesFromPoints :: (Point, Point) -> Set Curve circlesFromPoints (p1, p2) = Set.fromList [Circle p1 r, Circle p2 r] where r = dist p1 p2 curvesFromPoints :: (Point, Point) -> Set Curve curvesFromPoints pts = Set.insert (lineFromPoints pts) (circlesFromPoints pts) intersectionPoints :: Curve -> Curve -> Set Point intersectionPoints (VerticalLine _) (VerticalLine _) = Set.empty intersectionPoints (VerticalLine x_0) (GeneralLine m b) = Set.singleton (x_0, m*x_0 + b) intersectionPoints (GeneralLine m b) (VerticalLine x_0) = intersectionPoints (VerticalLine x_0) (GeneralLine m b) intersectionPoints (GeneralLine m_1 b_1) (GeneralLine m_2 b_2) = if m_1 == m_2 then Set.empty else Set.singleton (x_0,y_0) where x_0 = -(b_2 - b_1)/(m_2 - m_1) y_0 = m_1*x_0 + b_1 -- copy/pasted intersectionPoints (Circle (x_0, y_0) r_0) (Circle (x1,y1) r1) | d > r_0 + r1 = Set.empty | d < abs (r_0 - r1) = Set.empty | d == 0 && r_0 == r1 = Set.empty | otherwise = let a = (r_0^2 - r1^2 + d^2) / (2 * d) h = sqrt (r_0^2 - a^2) x2 = x_0 + a * (x1 - x_0) / d y2 = y_0 + a * (y1 - y_0) / d rx = -(y1 - y_0) * (h / d) ry = (x1 - x_0) * (h / d) in Set.fromList [(x2 + rx, y2 + ry), (x2 - rx, y2 - ry)] where dx = x1 - x_0 dy = y1 - y_0 d = sqrt (dx^2 + dy^2) intersectionPoints (Circle (h, k) r) (VerticalLine x) = intersectionPoints (VerticalLine x) (Circle (h, k) r) -- copy/pasted intersectionPoints (VerticalLine x) (Circle (h, k) r) = let dx = x - h radicand = r^2 - dx^2 in if radicand < 0 then Set.empty else let sqrtPart = sqrt radicand y1 = k + sqrtPart y2 = k - sqrtPart in if sqrtPart == 0 then Set.singleton (x, y1) else Set.fromList [(x, y1), (x, y2)] intersectionPoints (Circle (h, k) r) (GeneralLine m b) = intersectionPoints (GeneralLine m b) (Circle (h, k) r) -- copy/pasted intersectionPoints (GeneralLine m b) (Circle (h, k) r) = let a = 1 + m^2 b' = 2 * (m * (b - k) - h) c = h^2 + (b - k)^2 - r^2 discriminant = b'^2 - 4 * a * c in if discriminant < 0 then Set.empty else let sqrtD = sqrt discriminant x1 = (-b' + sqrtD) / (2 * a) x2 = (-b' - sqrtD) / (2 * a) y1 = m * x1 + b y2 = m * x2 + b in if sqrtD == 0 then Set.singleton (x1, y1) else Set.fromList [(x1, y1), (x2, y2)] pairs :: Set b -> [(b, b)] pairs xSet = [ (x, y) | (x:ys) <- tails xs, y <- ys ] where xs = Set.toList xSet new :: ((Point, Point) -> Set Curve) -> Diagram -> Set Curve new f (points, curves) = Set.difference allCurves curves where allCurves = foldl Set.union curves $ map f $ pairs points newCircles :: Diagram -> Set Curve newCircles = new circlesFromPoints newCurves :: Diagram -> Set Curve newCurves = new curvesFromPoints childDiagram :: Diagram -> Curve -> Diagram childDiagram (points, curves) curve = (childPoints, childCurves) where newPoints = flatMap (intersectionPoints curve) curves childPoints = Set.union points newPoints childCurves = Set.insert curve curves children :: (Diagram -> Set Curve) -> Diagram -> Set Diagram children new d = Set.map (childDiagram d) (new d) distinctDistances :: Set Point -> Set Construct distinctDistances ps = Set.fromList distanceList where distanceList = [dist p1 p2 | (p1:p2s) <- tails p1s, p2 <- p2s] p1s = Set.toList ps initialState :: Set Diagram initialState = Set.singleton (Set.fromList [(0,0), (0,1)], Set.empty) compassConstructions :: [Set Diagram] compassConstructions = iterate (flatMap $ children (new circlesFromPoints)) initialState rulerAndCompassConstructions :: [Set Diagram] rulerAndCompassConstructions = iterate (flatMap $ children (new curvesFromPoints)) initialStateThen we can compute A383082–A383087 with as the following:
a383082_list = map Set.size rulerAndCompassConstructions a383083_list = map Set.size compassConstructions a383084_list = map (Set.size . flatMap fst) rulerAndCompassConstructions a383085_list = map (Set.size . flatMap fst) compassConstructions a383086_list = map (Set.size . flatMap (distinctDistances . fst)) rulerAndCompassConstructions a383087_list = map (Set.size . flatMap (distinctDistances . fst)) compassConstructions
