Blog
-
G4G15 gift exchange: Parity Triangles from the OEIS
In February 2024, I attended the Gathering 4 Gardner in Atlanta (G4G15), which has a tradition of a gift exchange, where you bring 170 copies of a small gift, and in turn you get a small gift from all of the exchange participants.
One of these gifts, a set of 3D-printed fractals from Hideki Tsuiki appeared recently in the Numberphile video on the right—I have copies of these fractals in my office!
My G4G15 gift
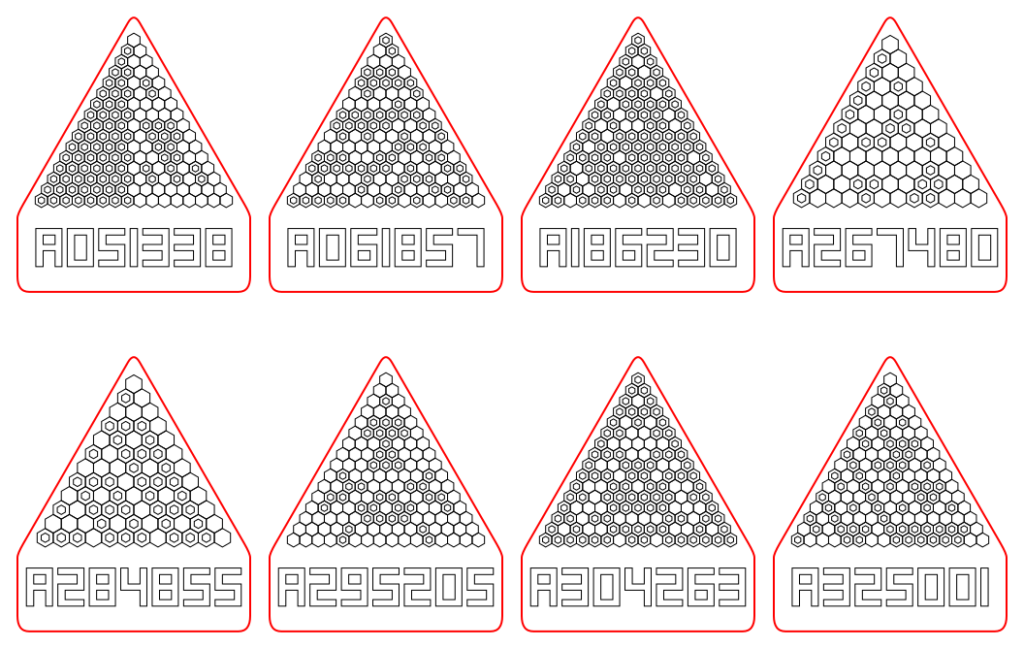
For my G4G15 gift, I made 200 distinct cards illustrating “parity triangles” of OEIS sequences, based on the idea in my blog post “Parity Bitmaps from the OEIS.”
Here’s how the cards turned out:


I used a Cricut to cut out the shapes of the cards, and then I draw them using an AxiDraw V3 pen plotter.

I then wrote a Python script that downloaded the data from the OEIS and generated SVG instructions for drawing the cards.
Here’s a video (sped up by a factor of 10x) showing the AxiDraw V3 pen plotter dutifully following the instructions.

Send me a message on Bluesky @peterkagey.com if you want me to put one in the mail for you!
-
Yan Zhang on power and Conway
You know that feeling when someone expresses a feeling that you have better than you ever could figure out how to articulate it? While archiving my old liked tweets, I noticed that Yan Zhang had done it. Twice.
I wanted to make sure that I copied these notes down so that I could still reference these ideas even now that I’ve left Twitter.
On status
I learned about this thread via Francis Su. Here Yan writes about status and power inside (and outside) the mathematical universe, by sharing a painful story where he overheard a student dismissing his career path which emphasized teaching and mentoring.

Here’s the story that Yan describes as “a very personal traumatic experience that I am still working to overcome,” and says, “tl;dr; I have no regrets, except this single experience that represents a force in the world that is powerful, destructive, and unnerving.”
Nearly 100% of people w/ my background (elite-level math BA and PhD degrees) either went to high-tier (R1) research universities or exitted into finance, tech, or startups. I work at a state school and barely pay the bills. I am fulfilled by my job and side projects.
One of those side projects is SPARC, a summer program I run for gifted youth. I helped organize it for over 10 years. (For people not in the know, doing this stuff is *not* helpful for your CV in academia; it’s like teaching awards — your hiring committee won’t care.
Weird — why don’t *universities* care about teaching? The way the status sausage is made is people want “objective” proofs of ability to bring objective money and fame to the dept. Teaching is “nice” but doesn’t bring money and fame to the dept. So they don’t care, QED.)
Anyway, I’m at a non-elite place where people actually appreciate (or at least doesn’t actively scoff at) these things; I spend a lot of time mentoring my “normal” students there and “gifted” students at SPARC. A diversified portfolio, since *both* types are important!
I spent a lot of time on one of the SPARC students. To hide identity, let’s say it’s a “he.” I was the one who interviewed him. I felt he was super talented, though socially awkward. Through some deliberation, we ended up accepting him. We got what we expected: smart, but loud and often detrimental to the discussions. I personally spent a ton of extra hours on him to help him “play nice” with the community, since the community offered him a lot of love and support. We repeated this for another year, it was exhausting, but I had hope.
In particular, I had hope that the values of our community got to him: it’s not just about how smart you are or what your “intellectual status” is. It’s about seeing each other as people, nurturing each other, doing good things in the world.
I thought I got through to him.
Seasoned educators would sigh here: “you never ‘really get through’ to people. Reality isn’t that clean.” I know, I know. This example was a case in point. Clearly this lesson never “got through” to myself. 😩
Fast forward a couple of years, I meet him at some event with a few other MIT kids, some SPARC alumni and a few new faces. I was in a mentor role, so I was mostly sharing my experiences. Tired, but having a good time. Then I overhear him talking w/ some other kids.
It started off generic: the same old stuff about grades, grad school, how to succeed later, conversations he probably have (and I probably myself had) hundreds of times. He’s going to be a PhD at an elite place and he wants to be a professor afterwards. I did too.
“Yeah, I really want to avoid ending up where Yan is.” (even typing these (probably inaccurate) words made my stomach ache. I get that feeling very rarely. It reminded me of heartbreak or tilting away hundreds of dollars on a poker hand: Sickness. “Why?” Regret. Anger.)
Then, just to twist the knife a bit, another SPARC alum nodded and agreed with him. “Yeah I know what you mean.” Countless things flooded my mind: My high school contest successes. My “elite” degrees. When I got my teaching award. When a colleague belittled my award. When I left math for finance. When I decided to return, trading $ for beauty, for happiness. Smiling SPARC kids, talking about emotions and lives instead of “success.” My inspirations (like @FedericoArdila and @mathyawp ) who put love in teaching instead of CV-boosting SPARC kids who told me “thanks for showing me there are things other than competition”. My amazing state school students who learned math while supporting their parents. My R1 colleague who unironally boasted about scaring students off so he can work during office hours.
I sat down somewhere and just cried.
The tears wouldn’t stop coming out.
I’m crying myself typing these words. It’s just too complicated.
“Regret” is probably the wrong word. It’s more “powerlessness.”
Status, or “proof of success,” gives us humans ability to recognize work. It also gives us an objective metric to optimize. With optimization comes the rat race. It’s like money. Money gives us ability to trade liquidly. And also an objective metric to optimize.Status leads many, many talented youth to chase a few small things. All that energy to outcompete your friends so you can get to a stronger school. All that energy to get to a better postdoc. All that energy to get to a higher position at Google.
And like all ideological fetishes, it protects itself. If someone wise person tries to show me that I was blinded by status, my first instinct is probably to check that person’s status to see if he should be “allowed” to speak.
It felt like fighting an Elder God, like Poverty or Inequality. I couldn’t just destroy a core. I was wrestling against human nature and the cold, hard truths of incentives. Before Status, I felt (and still feel) powerless.I think I’ve found myself doing a lot of sense-making over the past few years with respect to Yan’s lens here—and it seems to have especial explanatory power for me now in grappling with the the post-2024 political landscape.
“Why John Conway gets no recognition”
I want to put that thread in conversation with another thread that Yan wrote a few months earlier—the way that the pursuit of status (and jobs) manifests in the math research world sometimes devalues certain kinds of intellectual pursuits that aren’t “serious,” even if the corresponding problems are every bit as difficult, and especially when the problems are interesting to a non-specialist audience.
The thread comes in response to the article “John Conway Solved Mathematical Problems With His Bare Hands” in Quanta by Kevin Hartnett.


Thread to explain why Conway gets no recognition. Thesis: what is considered “important” in pure mathematics is purely a social construct. Corollary: why Conway doesn’t get recognition from mathematicians. Now that I have triggered some, I’ll explain.
First, pure mathematicians are not (usually) conspiring to make pyramid schemes — in fact, most of them are good-hearted people earnestly trying to ask themselves fundamental questions. However, this does not mean they’re immune to groupthink and idea-incest.
Second, pure math fundamentally lacks “skin in the game” in form of a relationship with the real world (and as we often see from physics or statistics, even those fields entangled with the real world can fail spectacularly when the incentive structures aren’t well-designed).
Third, pure math has a very high barrier to entry, and thus lacks critics who are knowledgeable enough to say something interesting. This means most criticism must come from its own practitioners, which creates incest. Now, let’s see what happens when we mix these three.
First, a field gains initial success, solving 90% of the fundamental questions (that are often quite “easy” technically). Then, they become pyramid schemes (often, but not always, with no sociopathic figurehead), this is self-justified since you need new Ph D. students.
Finally, the language and *taste* calcifies. Now there’s an idea of what math is “good” or “cool.” These aren’t testable or objective. They can’t be. These are organic social constructs.
In short, when wise people say “math is a social construct,” they don’t mean the *veracity* of math. They’re talking about the *importance*. Here is where Conway falters (for his colleagues) and delights (for everyone else): Conway did any mathematics he thought interesting.
By doing this, he is showing irreverence for the social norms other mathematicians have created as “important.” As all of us know, when you act as if you don’t care about what others seem “cool,” you become “uncool.” And that’s exactly what happened with (some) mathematicians.
They know he has technical chops and is an excellent problem solver *and* theory builder. But he’s doing those things with games, pictures, weird number sequences. He’s not doing those things with cohomology, sheaves, derived functors.
They aren’t necessarily even jealous; they’re just confused. “Why isn’t someone who is *able* to do these things doing them? Why is he wasting time?”
Sometimes they will (again, with completely good intentions) tell Conway and/or people like him “you know, with your talents you can probably do some pretty important work.” (I myself have gotten these comments, while doing “unimportant” work like consulting or blockchain)
So when Conway does his (amazing) work, he’s really doing it as a “people’s mathematician.” He’s doing what *he* sees as fun and important, which makes it a more “vulgar” form of mathematics. For professional mathematicians trained on “classy” mathematics, their taste buds have also been trained (from their socially-constructed groups) to see “vulgar” math as less important, much in the way that a 90’s classical TV critic may judge South Park or the Simpsons as “mainstream trash,” or, as something deeply close to my heart, people saying that “videogames cannot be art.” When they play videogames, their brain is *trained* to tell them that this is *supposed* to be bad, because “respectable” people are not playings games but are reading books, or so they think. We mathematicians are no different. RIP. -
LEGO Truchet
In the process of going through my old saved tweets as I transition away from Twitter, I saw this tweet from Dave Richeson who is now posts on Bluesky as @divbyzero.bsky.social. About one year after this, I made a LEGO Truchet tiling for Dave, not realizing that I had probably been unconsciously inspired by his!

Mastodon
Recently I saw a post on Mathstodon from @diamabolo, which goes a step further: a LEGO Truchet Tile Machine!
Stud.io
When I went to make my own LEGO Truchet, I used LEGO Studio to make some digital mockups, find the part numbers, and by the pieces in bulk via Bricklink.









LEGO Truchet in the physical world
I ordered 172.46€ worth of parts from Germany—enough to make eight different tilings, three of which are shown below.



Building for Dave Richeson
One tiling was based on a post by Dave Richeson’s bot @randomtiling.bsky.social, which I mailed to him. Here’s a picture of the work-in-progress.

The design was based on an actual post from Random Tiling Bot (@randomtiling), which I can’t find now. This one is close enough:
LEGO part numbers
The 10 x 10 Truchet tiling I made for Dave is made from two different LEGO parts together with a 32 x 32 gray baseplate.
- Part 25269 — Tile, Round 1 x 1 Quarter
- Part 3396 — Tile, Modified 2 x 2 with 2 1 x 1 Curved Cutouts (Double Arrow)




