
Hello! I’m Peter!
Blog
-
Straightedge and Compass Constructions (1 of 2)
How many distinct constructions can be made with a straightedge and compass if we draw \(n\) lines and circles?
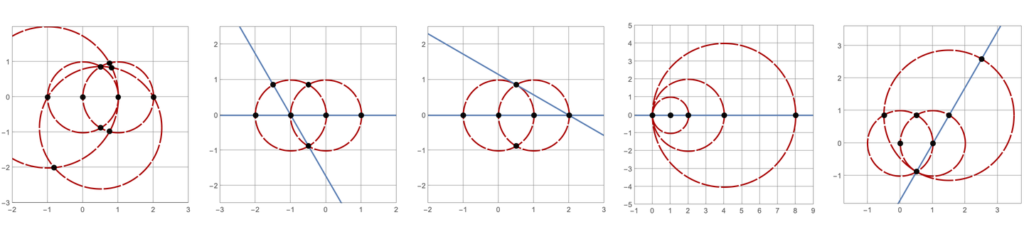
An example of five straightedge-and-compass constructions each with \(5\) lines and circles. Describing a straightedge-and-compass construction
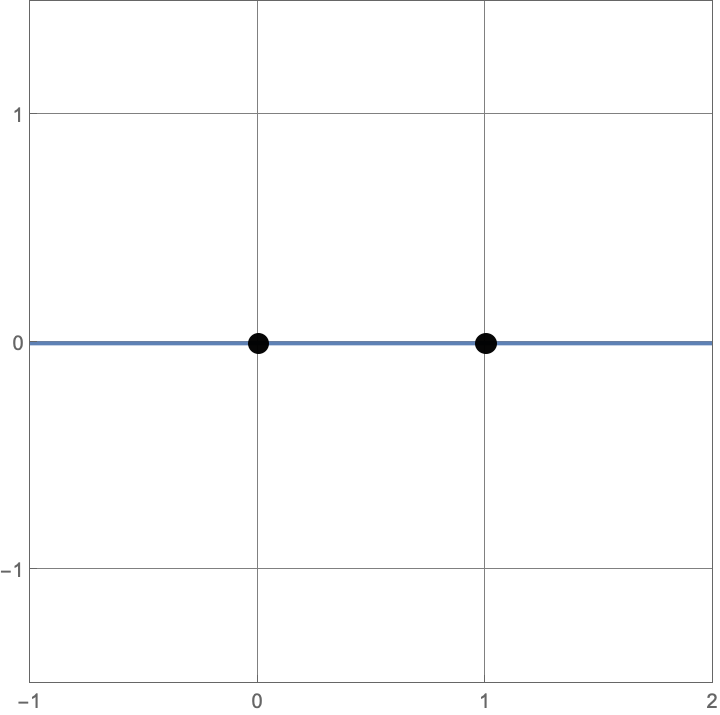
Initially we start with two points, which we call \((0,0)\) and \((1,0)\). At each step, we can do one of two things:
- Straightedge. We can use the straightedge to draw the line connecting any two points.
- Compass. We can place the needle of a compass at a point \(p_1\), and the other tip at another point \(p_2\), and draw the circle centered at \(p_1\) that goes through \(p_2\)
We get new points whenever lines intersect with lines, lines intersect with circles, or circles intersect with circles.
The On-Line Encyclopedia of Integer Sequences (OEIS)
I’ve added this to the OEIS as sequence A383082, which begins $$1, 3, 3, 16, 205, 5886, 542983, \dots.$$ I’ve illustrated some of the terms of this sequence here.
There’s a theorem, the Mohr–Mascheroni theorem, which states that any points that can be constructed with a straightedge and compass, can be constructed with a compass alone. This is the motivation for OEIS as sequence A383083, which gives the number of constructions with \(n\) circles and no lines and begins $$1, 2, 1, 4, 44, 1084, 91192, \dots.$$
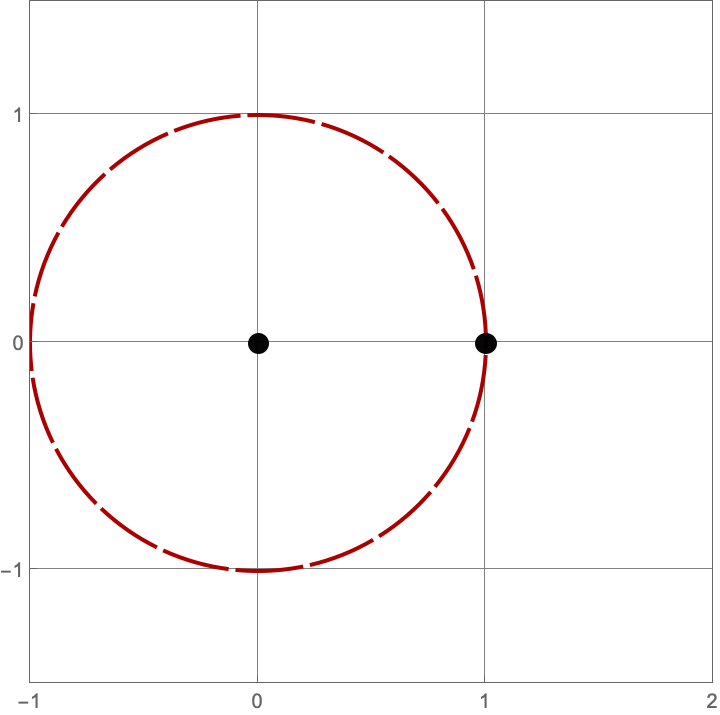
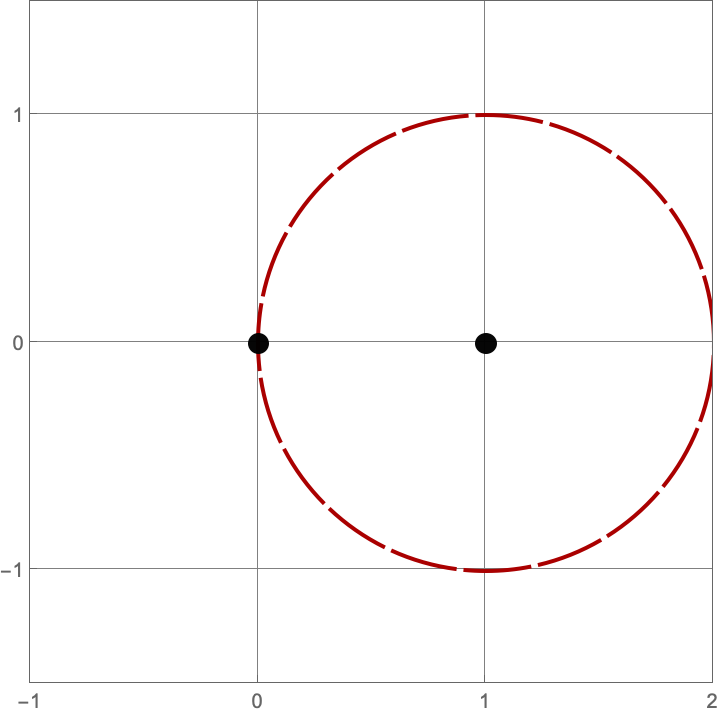
\(A383082(1) = 3\)
Here are the three constructions with one line or circle.
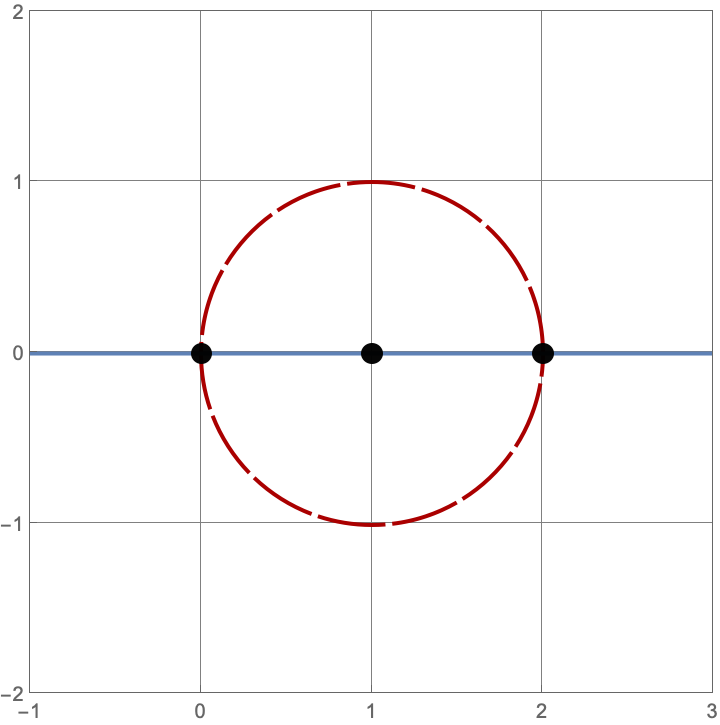
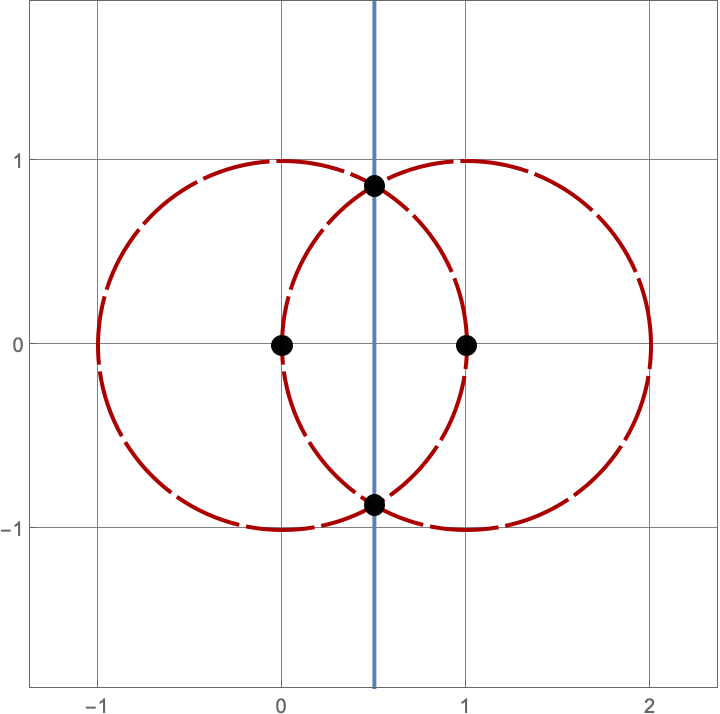
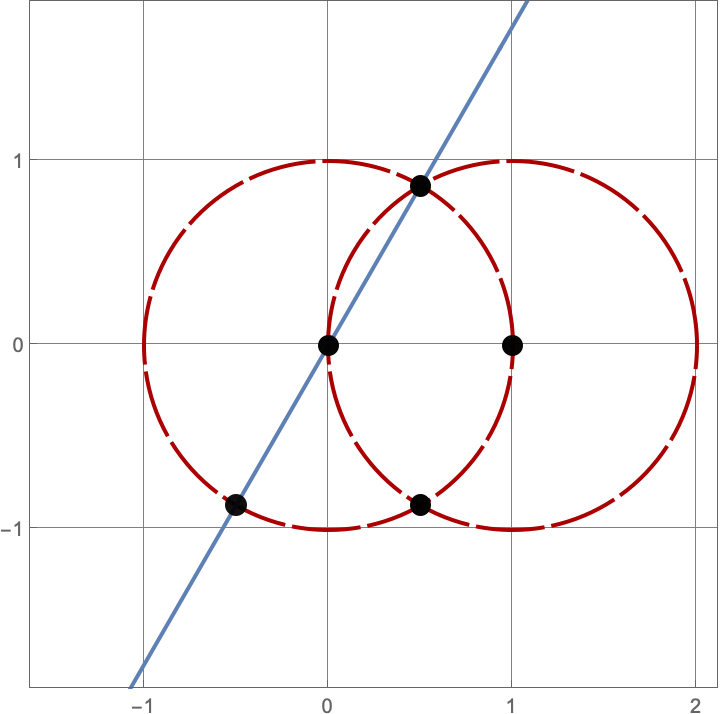
\(A383082(2) = 3\)
Here are the three constructions with two lines and circles.

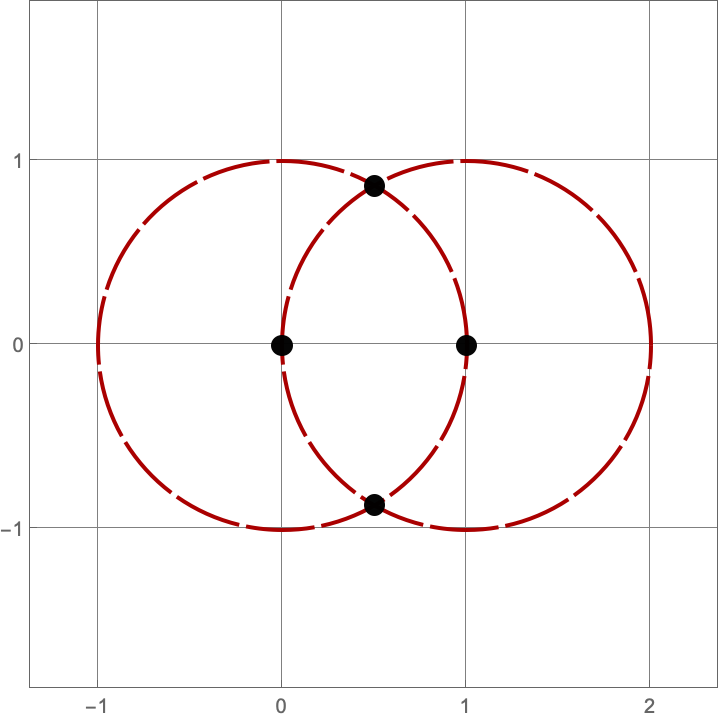
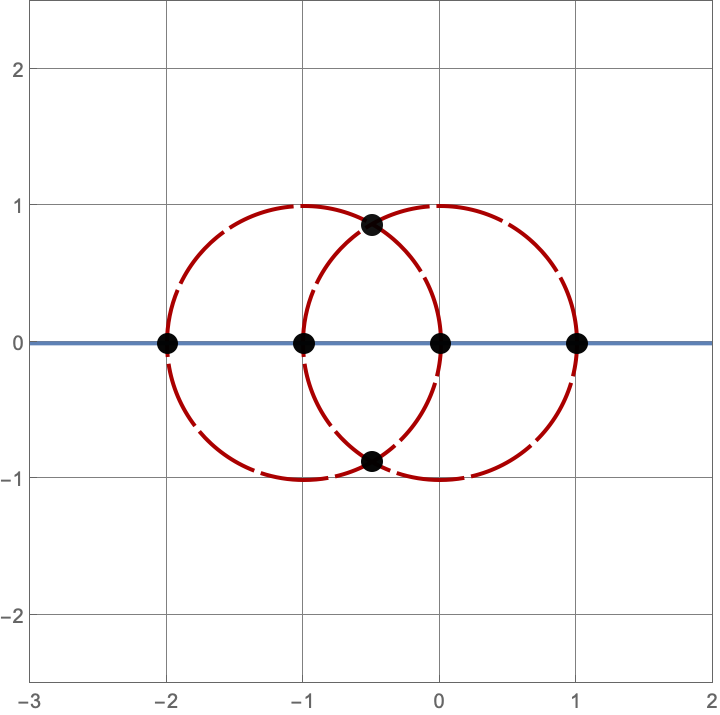
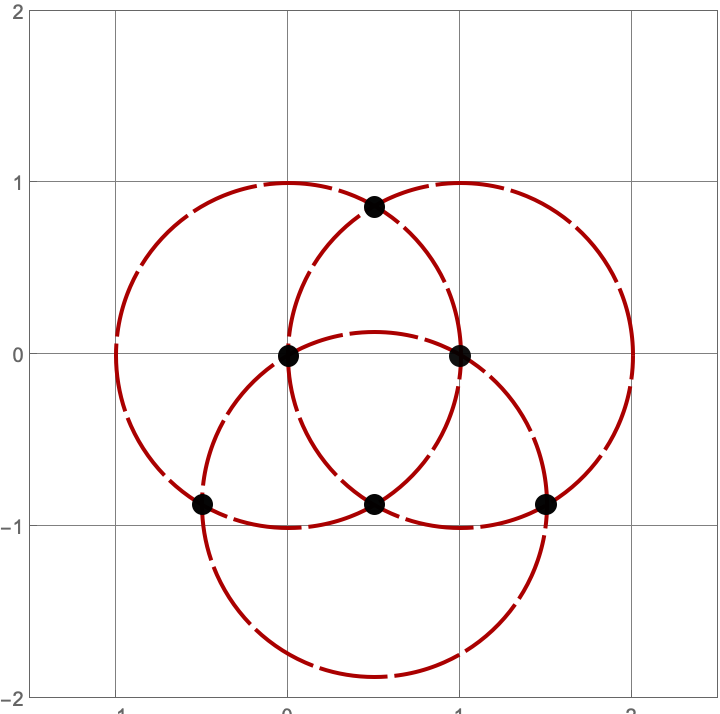
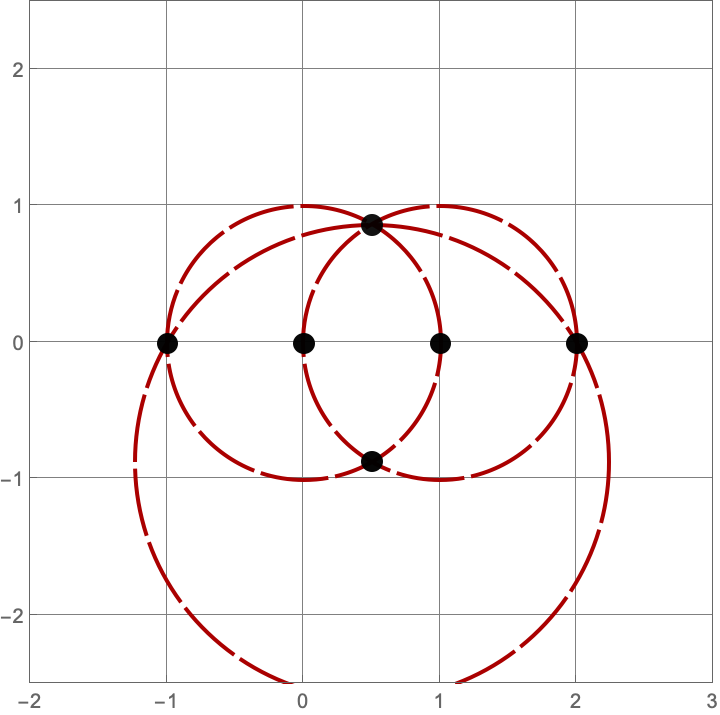
\(A383082(3) = 16\)
Here are the sixteen constructions with three lines and circles.
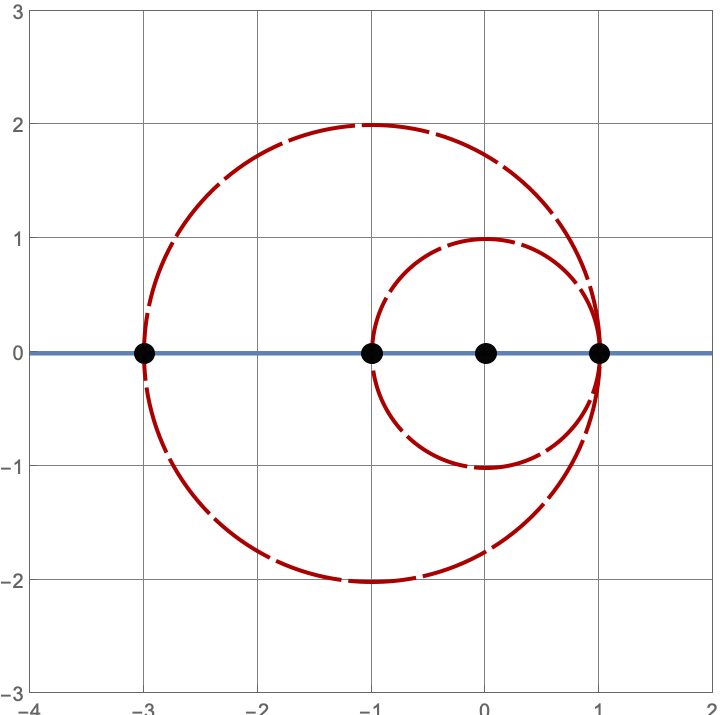
\(A383082(4) = 205\)
There are \(\operatorname{A383082}(4) = 205\) constructions with \(4\) lines and circles. Here’s a sample of five such constructions. Click on the image to see all \(205\) of them.

\(n\le5\)
Watch the video below to see all \(1 + 3 + 3 + 16 + 205 + 5886 = 6114\) constructions with \(5\) or fewer lines and circles played at 60 fps for 1.7 minutes.
Computing the sequences
In total, I computed six sequence, which I submitted to the OEIS:
- A383082: The number of distinct straightedge-and-ruler constructions that can be made with a total of \(n\) lines and circles. $$1, 3, 3, 16, 205, 5886, 542983$$
- A383083: The number of distinct straightedge-and-compass constructions that can be made with no lines and \(n\) circles.$$1, 2, 1, 4, 44, 1084, 91192$$
- A383084: The number of points in the Euclidean plane that can be determined via a straightedge-and-compass construction using \(n\) or fewer lines and circles. $$2, 2, 6, 14, 147, 5743$$
- A383085: The number of points in the Euclidean plane that can be determined via a straightedge-and-compass construction using no lines and \(n\) or fewer circles. $$2, 2, 4, 10, 52, 1704, 214135$$
- A383086: The number of distinct distances between points in the Euclidean plane where the points are constructed via a straightedge-and-compass construction using \(n\) lines and no circles. $$1, 1, 2, 4, 35, 2480$$
- A383087: The number of distinct distances between points in the Euclidean plane where the points are constructed via a straightedge-and-compass construction using \(n\) lines and circles. $$1, 1, 3, 5, 73, 6628$$
(I’m most optimistic about being able to extend A383084. I’m least optimistic about being able to extend A383083.)
Haskell code
I computed the sequence originally in Mathematica and then checked my work in Haskell using Anders Kaseorg’s library Constructible. Here’s the Haskell code that I used to compute the OEIS sequences.
module Helpers.RulerAndCompass (rulerAndCompassConstructions, compassConstructions, distinctDistances) where import Data.Real.Constructible (Construct) import Data.Set (Set) import qualified Data.Set as Set import Data.List (tails) import Helpers.SetHelpers (flatMap) type Diagram = (Set Point, Set Curve) type Point = (Construct, Construct) data Curve = VerticalLine Construct -- x_0 | GeneralLine Construct Construct -- m & b for | Circle Point Construct deriving (Show, Eq, Ord) lineFromPoints :: (Point, Point) -> Curve lineFromPoints ((x1,y1), (x2,y2)) = if x1 == x2 then VerticalLine x1 else GeneralLine m b where m = (y2-y1)/(x2-x1) b = (x2*y1 - x1*y2)/(x2-x1) dist (x1,y1) (x2,y2) = sqrt ((x2 - x1)^2 + (y2 - y1)^2) circlesFromPoints :: (Point, Point) -> Set Curve circlesFromPoints (p1, p2) = Set.fromList [Circle p1 r, Circle p2 r] where r = dist p1 p2 curvesFromPoints :: (Point, Point) -> Set Curve curvesFromPoints pts = Set.insert (lineFromPoints pts) (circlesFromPoints pts) intersectionPoints :: Curve -> Curve -> Set Point intersectionPoints (VerticalLine _) (VerticalLine _) = Set.empty intersectionPoints (VerticalLine x_0) (GeneralLine m b) = Set.singleton (x_0, m*x_0 + b) intersectionPoints (GeneralLine m b) (VerticalLine x_0) = intersectionPoints (VerticalLine x_0) (GeneralLine m b) intersectionPoints (GeneralLine m_1 b_1) (GeneralLine m_2 b_2) = if m_1 == m_2 then Set.empty else Set.singleton (x_0,y_0) where x_0 = -(b_2 - b_1)/(m_2 - m_1) y_0 = m_1*x_0 + b_1 -- copy/pasted intersectionPoints (Circle (x_0, y_0) r_0) (Circle (x1,y1) r1) | d > r_0 + r1 = Set.empty | d < abs (r_0 - r1) = Set.empty | d == 0 && r_0 == r1 = Set.empty | otherwise = let a = (r_0^2 - r1^2 + d^2) / (2 * d) h = sqrt (r_0^2 - a^2) x2 = x_0 + a * (x1 - x_0) / d y2 = y_0 + a * (y1 - y_0) / d rx = -(y1 - y_0) * (h / d) ry = (x1 - x_0) * (h / d) in Set.fromList [(x2 + rx, y2 + ry), (x2 - rx, y2 - ry)] where dx = x1 - x_0 dy = y1 - y_0 d = sqrt (dx^2 + dy^2) intersectionPoints (Circle (h, k) r) (VerticalLine x) = intersectionPoints (VerticalLine x) (Circle (h, k) r) -- copy/pasted intersectionPoints (VerticalLine x) (Circle (h, k) r) = let dx = x - h radicand = r^2 - dx^2 in if radicand < 0 then Set.empty else let sqrtPart = sqrt radicand y1 = k + sqrtPart y2 = k - sqrtPart in if sqrtPart == 0 then Set.singleton (x, y1) else Set.fromList [(x, y1), (x, y2)] intersectionPoints (Circle (h, k) r) (GeneralLine m b) = intersectionPoints (GeneralLine m b) (Circle (h, k) r) -- copy/pasted intersectionPoints (GeneralLine m b) (Circle (h, k) r) = let a = 1 + m^2 b' = 2 * (m * (b - k) - h) c = h^2 + (b - k)^2 - r^2 discriminant = b'^2 - 4 * a * c in if discriminant < 0 then Set.empty else let sqrtD = sqrt discriminant x1 = (-b' + sqrtD) / (2 * a) x2 = (-b' - sqrtD) / (2 * a) y1 = m * x1 + b y2 = m * x2 + b in if sqrtD == 0 then Set.singleton (x1, y1) else Set.fromList [(x1, y1), (x2, y2)] pairs :: Set b -> [(b, b)] pairs xSet = [ (x, y) | (x:ys) <- tails xs, y <- ys ] where xs = Set.toList xSet new :: ((Point, Point) -> Set Curve) -> Diagram -> Set Curve new f (points, curves) = Set.difference allCurves curves where allCurves = foldl Set.union curves $ map f $ pairs points newCircles :: Diagram -> Set Curve newCircles = new circlesFromPoints newCurves :: Diagram -> Set Curve newCurves = new curvesFromPoints childDiagram :: Diagram -> Curve -> Diagram childDiagram (points, curves) curve = (childPoints, childCurves) where newPoints = flatMap (intersectionPoints curve) curves childPoints = Set.union points newPoints childCurves = Set.insert curve curves children :: (Diagram -> Set Curve) -> Diagram -> Set Diagram children new d = Set.map (childDiagram d) (new d) distinctDistances :: Set Point -> Set Construct distinctDistances ps = Set.fromList distanceList where distanceList = [dist p1 p2 | (p1:p2s) <- tails p1s, p2 <- p2s] p1s = Set.toList ps initialState :: Set Diagram initialState = Set.singleton (Set.fromList [(0,0), (0,1)], Set.empty) compassConstructions :: [Set Diagram] compassConstructions = iterate (flatMap $ children (new circlesFromPoints)) initialState rulerAndCompassConstructions :: [Set Diagram] rulerAndCompassConstructions = iterate (flatMap $ children (new curvesFromPoints)) initialStateThen we can compute A383082–A383087 with as the following:
a383082_list = map Set.size rulerAndCompassConstructions a383083_list = map Set.size compassConstructions a383084_list = map (Set.size . flatMap fst) rulerAndCompassConstructions a383085_list = map (Set.size . flatMap fst) compassConstructions a383086_list = map (Set.size . flatMap (distinctDistances . fst)) rulerAndCompassConstructions a383087_list = map (Set.size . flatMap (distinctDistances . fst)) compassConstructions
-
Torus tilings
Ever since Bill Keehn and I started writing our paper, “Counting Tilings of the 𝑛 × 𝑚 Grid, Cylinder, and Torus,” I’ve been noticing and taking photos of tiles that I see that exhibit interesting symmetries.














































My wife will sometimes kid on the square: “Whenever you take your phone out to take a picture of a tile, you also have to take a picture of me.”
CPP Job Talk
When I gave my job talk at CPP, I included some of these tiles in my most labor-intensive slide transition:
Random Tiling Bot
I used some of these photos to programmatically generate tilings, inspired by Dave Richeson’s (@divbyzero.bsky.social) Bluesky bot Random Tiling Bot.












Torus tilings on a torus
Mathematica code
Here’s the code for drawing the patterns on a torus:
faceImage = ImageCrop[Import["tiling_018.png"],1620/3];
torus[u_, v_, R_ : 2, r_ : 1] := {
(R + r Cos[v]) Cos[u],
(R + r Cos[v]) Sin[u],
r Sin[v]
};
frames = Table[
ParametricPlot3D[torus[u, v], {u, 0, 2 Pi}, {v, 0, 2 Pi},
TextureCoordinateFunction -> ({#4, #5 + a} &),
PlotStyle -> Texture[faceImage],
Mesh -> None, Lighting -> "Neutral",
Boxed -> False, Axes -> False, Method -> {"ShrinkWrap" -> True},
Background -> Black, ImageSize -> Large
],
{a, 0, 1 - 1/120, 1/120}
]Python Code
Here’s code that randomly picks one of the above tiles, and draws rotations and reflections of it in a n×m grid. (I saved the tile images under the path
/tiles/tile_000.png.)from PIL import Image import random import os current_dir = os.path.dirname(os.path.abspath(__file__)) tiling_path = current_dir + "/generated/" generation = len(os.listdir(tiling_path)) gen_string = str(generation).zfill(3) random.seed(generation) path = current_dir + "/tiles/" tile_name = random.choice([f for f in os.listdir(path) if f[-3:]=="png"])[0:-4] big_tile_design = Image.open(path + tile_name + ".png") tile_design = big_tile_design.resize((180, 180), Image.LANCZOS) (n,m) = (3,3) # n × m torus canvas = Image.new("RGB", (180*n*3, 180*m*3)) tile_symmetries = [ tile_design, tile_design.rotate(90), tile_design.rotate(180), tile_design.rotate(270), tile_design.transpose(Image.FLIP_LEFT_RIGHT), tile_design.transpose(Image.FLIP_LEFT_RIGHT).rotate(90), tile_design.transpose(Image.FLIP_LEFT_RIGHT).rotate(180), tile_design.transpose(Image.FLIP_LEFT_RIGHT).rotate(270) ] tiles = random.choices(tile_symmetries, k=n*m) for j in range(m*3): for i in range(n*3): tile_choice = tiles[n*(j%m) + (i%n)] canvas.paste(tile_choice, (i * 180, j * 180)) canvas.save(tiling_path + "tiling_" + gen_string + ".png")Maybe I’ll make a bot? 😏
-
Fibonachos
A few weeks ago I was going through my saved tweets, and I saw this one from Math Lady Hazel which reminded me of a story from early 2017 that I played a small part in.
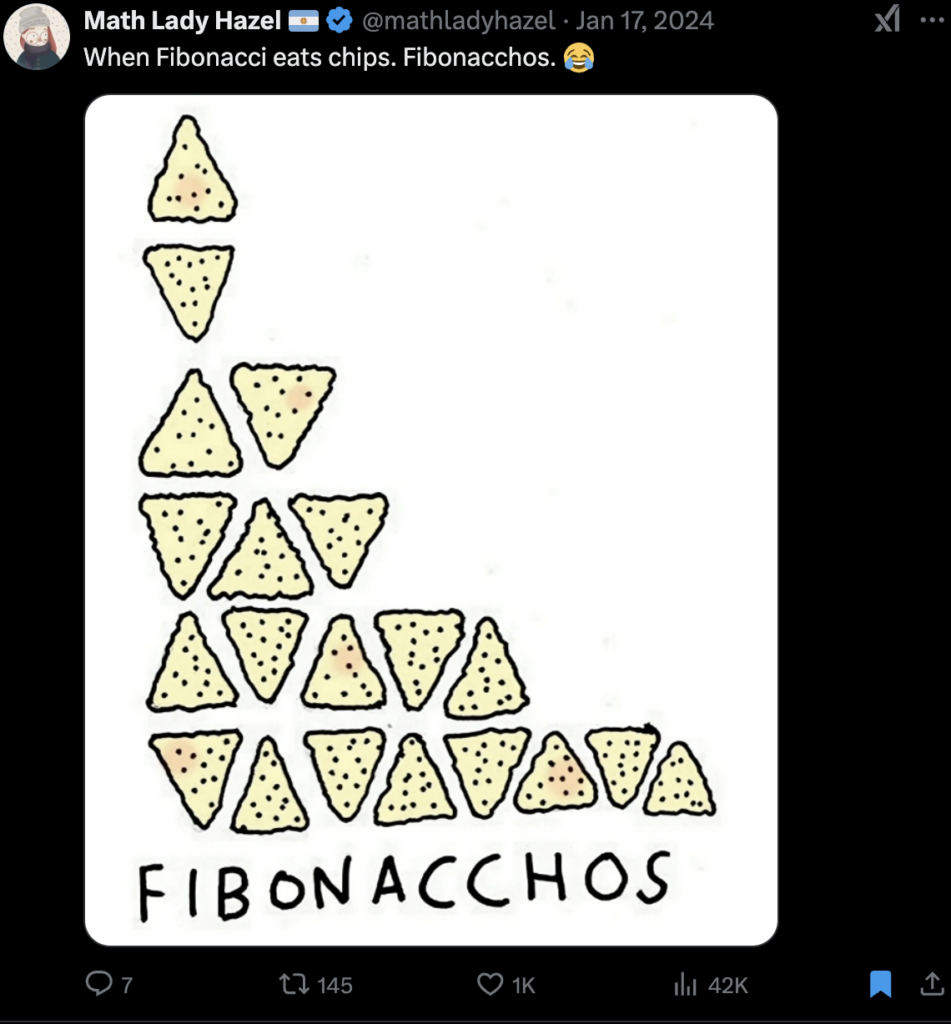
In January 2017, reddit user Teblefer asked the following question:
Two people are sharing a plate of nachos. They take turns dividing the nachos, each taking the nth Fibonacci number of nachos on the nth turn. When the number of nachos left is less than the next Fibonacci number, they start the sequence over. What number of nachos (less than 500) requires the most number of restarts? How would you generate numbers of nachos with a high number of restarts?
I computed the first few terms, added them to the OEIS as A280521 and A280523, and wrote:
I’m shocked that I didn’t find this sequence in the OEIS!
a(1) = 1 via [1] a(2) = 1 via [1, 1] a(3) = 2 via [1, 1], [1] a(4) = 1 via [1, 1, 2] a(5) = 2 via [1, 1, 2], [1] a(6) = 2 via [1, 1, 2], [1, 1] a(7) = 1 via [1, 1, 2, 3] a(8) = 2 via [1, 1, 2, 3], [1] a(9) = 2 via [1, 1, 2, 3], [1, 1] a(10) = 3 via [1, 1, 2, 3], [1, 1], [1] a(11) = 2 via [1, 1, 2, 3], [1, 1, 2] a(12) = 1 via [1, 1, 2, 3, 5]Here are where records appear (I also didn’t find this in the OEIS):
a(1) = 1 a(3) = 2 a(10) = 3 a(30) = 4 a(84) = 5 a(227) = 6 a(603) = 7 a(1589) = 8 a(4172) = 9Conjecture: Records appear at A215004(2n).
A215004(0) = A215004(1) = 1; for n>1, A215004(n) = A215004(n-2) + A215004(n-1) + floor(n/2).
Neil Sloane’s Winter Fruits
Later that month on January 26, 2017, Neil Sloane (the founder of the OEIS) gave a talk in Doron Zeilberger’s Experimental Mathematics Seminar at Rutgers titled “Winter Fruits: New Problems from OEIS December 2016–January 2017.” You can see a PDF of the slides here.
The lecture was recorded, and when I first got to the 12:50 minute mark, I was surprised to see my name appear on the screen.

Other nacho sequences
You can play the “Fibonachos” game for other sequences too, and Neil’s slides contained the following table:

\(S\) \(a(n)\) Records Fibonacci A280521 A280523 \(n\) A057945 A006893 \(\frac{n(n+1)}{2}\) A281367 A281368 \(2^n\) A100661 A000325 \(n^2\) A280053 A280054 Related sequences
While writing this post, I submitted OEIS sequence A382814: the number of Nachos that the first player gets.
A good rule of thumb is that the player who draws last before the first reset gets the greatest number of nachos.
I have a conjecture that I bet you could prove: let \(n\) be the number of nachos in the starting pile. When \(n > 32\), the last player to take nachos before “the number of nachos left is less than the next Fibonacci number, [and] they start the sequence over” is the player that ends up with the greatest number of nachos in the end.
Prove it, contribute the proof to the OEIS, and let me know on Bluesky @peterkagey.com.