
Hello! I’m Peter!
Blog
-
Vowel cascades
I saw a post on Bluesky that proposed a problem that I had been thinking about for a long time!
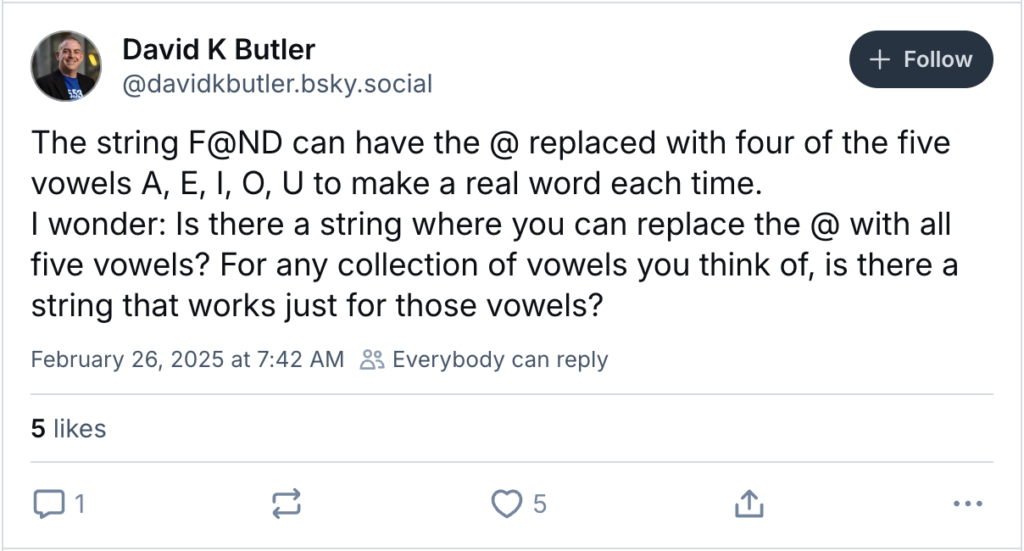
I figured that with the help of dictionary and a Python script, I could find the desired examples.
One vowel
- A: t_lk
- E: wh_n
- I: w_th
- O: fr_m
- U: cl_b
Two vowels
- AE: sm_ll
- AI: th_nks
- AO: d_wn
- AU: b_nk
- EI: m_nd
- EO: kn_w
- EU: j_st
- IO: sh_rt
- IU: sk_lls
- OU: sp_rt
Three vowels
- AEI: w_ll
- AEO: l_ss
- AEU: fl_sh
- AIO: t_p
- AIU: st_ff
- AOU: c_ts
- EIO: m_ld
- EIU: d_sk
- EOU: c_lts
- IOU: p_lls
Four vowels
- AEIO: r_d
- AEIU: b_ll
- AEOU: l_gs
- AIOU: m_st
- EIOU: d_ll
- AEIOU: b_t
Python code
Here’s my quick Python script to help find these. The dictionary has some words that I’m not familiar with (e.g. “cen,” “wir,” etc.) so I had to manually audit the results.
from wordfreq import top_n_list import re from collections import defaultdict common_words = top_n_list('en', 50000) def vowels(word): return re.findall(r'[aeiouy]', word, re.IGNORECASE) def has_one_vowel(word): return len(vowels(word)) == 1 def first_vowel(word): return vowels(word)[0] def replace_vowels(word): return re.sub(r'[aeiouyAEIOUY]', '_', word) one_vowel_words = filter(has_one_vowel, common_words) dict = defaultdict(list) for w in one_vowel_words: dict[replace_vowels(w)] = sorted(dict[replace_vowels(w)] + [first_vowel(w)]) vowel_subsets = [['a'], ['e'], ['i'], ['o'], ['u'], ['a', 'e'], ['a', 'i'], ['a', 'o'], ['a', 'u'], ['e', 'i'], ['e', 'o'], ['e', 'u'], ['i', 'o'], ['i', 'u'], ['o', 'u'], ['a', 'e', 'i'], ['a', 'e', 'o'], ['a', 'e', 'u'], ['a', 'i', 'o'], ['a', 'i', 'u'], ['a', 'o', 'u'], ['e', 'i', 'o'], ['e', 'i', 'u'], ['e', 'o', 'u'], ['i', 'o', 'u'], ['a', 'e', 'i', 'o'], ['a', 'e', 'i', 'u'], ['a', 'e', 'o', 'u'], ['a', 'i', 'o', 'u'], ['e', 'i', 'o', 'u'], ['a', 'e', 'i', 'o', 'u']] for vs in vowel_subsets: print("".join(vs).upper() + ":", ", ".join([k for k, v in dict.items() if v == vs][0:10])) -
Cube fractals
Robert Fathauer’s fractal
On May 16th, 2024, Robert Fathauer tweeted a wonderful timelapse video of building a white cube fractal, which you can see below.

When I tried to learn more about this fractal, I found a Mathematica demo called “Shifting Cube Fractal”. I couldn’t get the demo to work quite properly, so I illustrated it myself by writing a Mathematica script to make this video:
Bluesky #MathArtMarch
In March 2025, @ayliean.bsky.social started #MathArtMarch with a list of prompts to use to make new art or post existing art. On Day 12, I saw @curved-ruler.bsky.social‘s cube fractal, and inspired it, Ayliean’s prompt, and Robert Fathauer’s timelapse, I modified the above video to show off some new perspectives.
This video has four frames where the sides of the cube are perfectly transparent, and these look very reminiscent of @curved-ruler.bsky.social‘s cube fractal.



Mathematica code
Here’s my quick and dirty Mathematica code used to make the first illustration. If you modify it, show me what you make on Bluesky! (@peterkagey.com)
nextGen[cube_, t_] := (
s = Volume[cube]^(1/3)/2;
c = RegionCentroid[cube];
{
Cube[c + s {1.5, -0.5 + t, -0.5 + t}, s],
Cube[c + s {-1/2 + t, 1.5, -1/2 + t}, s],
Cube[c + s {-0.5 + t, -0.5 + t, 1.5}, s]
}
)
frames = Table[
cubes = {{Cube[]}};
cubes =
Append[cubes,
Flatten[nextGen[#, (Sin[2 \[Pi] t + \[Pi]/4] + 1)/2] & /@
cubes[[-1]]]];
cubes =
Append[cubes,
Flatten[nextGen[#, (Sin[2 \[Pi] t + \[Pi]/4] + 1)/2] & /@
cubes[[-1]]]];
cubes =
Append[cubes,
Flatten[nextGen[#, (Sin[2 \[Pi] t + \[Pi]/4] + 1)/2] & /@
cubes[[-1]]]];
cubes =
Append[cubes,
Flatten[nextGen[#, (Sin[2 \[Pi] t + \[Pi]/4] + 1)/2] & /@
cubes[[-1]]]];
Graphics3D[
Transpose[{Table[
Hue[(3 n)/5 + (Sin[2 \[Pi]*t] + 1)/10], {n, 1, 5}], cubes}],
ViewVector ->
100*{Sin[4 \[Pi]*t - \[Pi]/4], Sin[4 \[Pi]*t - \[Pi]/4],
Sqrt[2] Cos[4 \[Pi]*t - \[Pi]/4]},
ViewVertical -> -{Sin[4 \[Pi]*t + \[Pi]/4],
Sin[4 \[Pi]*t + \[Pi]/4], Sqrt[2] Cos[4 \[Pi]*t + \[Pi]/4]},
ViewAngle -> 0.025,
ImageSize -> {720, 720}, Boxed -> False, Lighting -> "Neutral",
SphericalRegion -> True],
{t, 1/200, 1, 1/200}
]
Export["frame_000.png", frames, "VideoFrames"] -
Saved video tweets (Part 4/4)
As I discussed in Part 1, Part 2, and Part 3, I’m going through my old saved tweets and documenting them as I move to Bluesky (@peterkagey.com). Here are the last three of those tweets (all of which had video/GIF embeddings):
- Alison Martin packing (2024-03-08)
- Matt Henderson on Pringles (2022-02-20)
- Lenore with a video of a human polyhedron (2024-06-15)
Alison Martin packing

Can anyone tell me more about the geometry of this? Let me know on Bluesky!
Matt Henderson on Pringles

I watched this 12 minute YouTube video (ad?) “How Pringles Are Made In Factory” to see if Pringles would ever be extruded through a “letterbox,” but alas, they are just stamped out using molds.
Also check out this Pringles tesselation that I learned about on Bluesky from @mathgrrl.bsky.social via @johngolden.bsky.social.

These tessellations are by @theo.rooden.art.weaving on Instagram—go over there and like and share!








Lenore with a video of a human polyhedron
No, not a human pyramid—a human rhombic dodecahedron. (I reached out to the Los Angeles Public Library to see if their librarians could help me to figure out where this comes from!)
I imagine them saying to each other, “If we put our heads together, we can make a rhombic dodecahedron.”

I made a model of the polyhedron that rotates, and where the participants “put their heads together” to alternate between a 13-face solid and a rhombic dodecahedron.