How many distinct constructions can be made with a straightedge and compass if we draw \(n\) lines and circles?
Describing a straightedge-and-compass construction
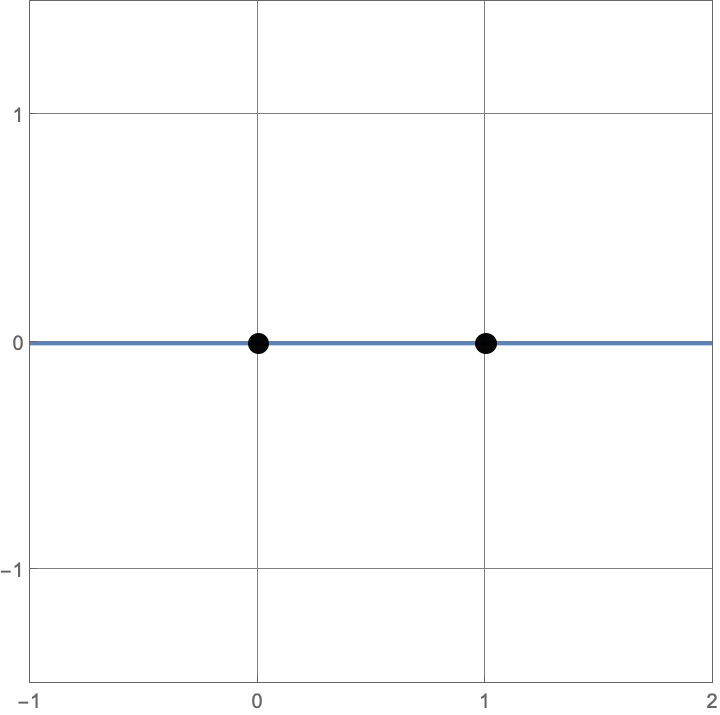
Initially we start with two points, which we call \((0,0)\) and \((1,0)\). At each step, we can do one of two things:
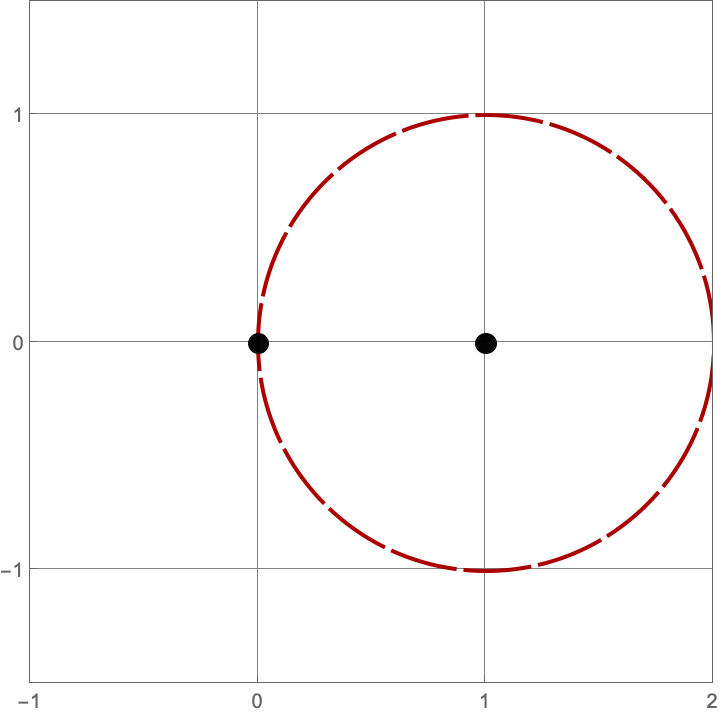
- Straightedge. We can use the straightedge to draw the line connecting any two points.
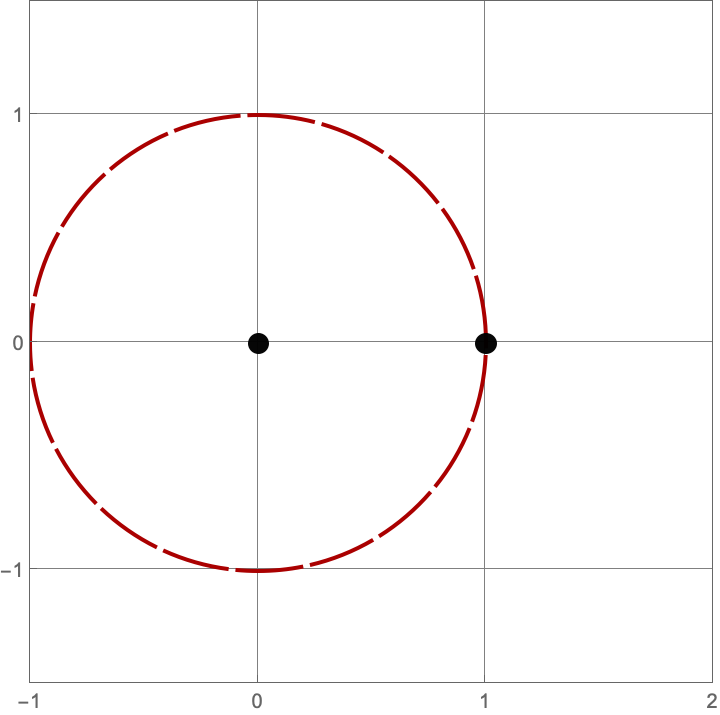
- Compass. We can place the needle of a compass at a point \(p_1\), and the other tip at another point \(p_2\), and draw the circle centered at \(p_1\) that goes through \(p_2\)
We get new points whenever lines intersect with lines, lines intersect with circles, or circles intersect with circles.
The On-Line Encyclopedia of Integer Sequences (OEIS)
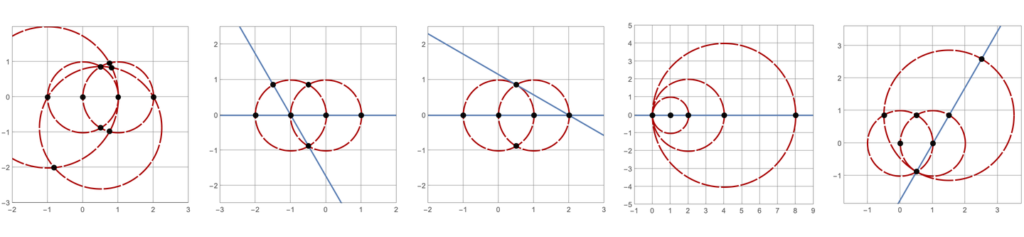
I’ve added this to the OEIS as sequence A383082, which begins $$1, 3, 3, 16, 205, 5886, 542983, \dots.$$ I’ve illustrated some of the terms of this sequence here.
There’s a theorem, the Mohr–Mascheroni theorem, which states that any points that can be constructed with a straightedge and compass, can be constructed with a compass alone. This is the motivation for OEIS as sequence A383083, which gives the number of constructions with \(n\) circles and no lines and begins $$1, 2, 1, 4, 44, 1084, 91192, \dots.$$
\(A383082(1) = 3\)
Here are the three constructions with one line or circle.
\(A383082(2) = 3\)
Here are the three constructions with two lines and circles.

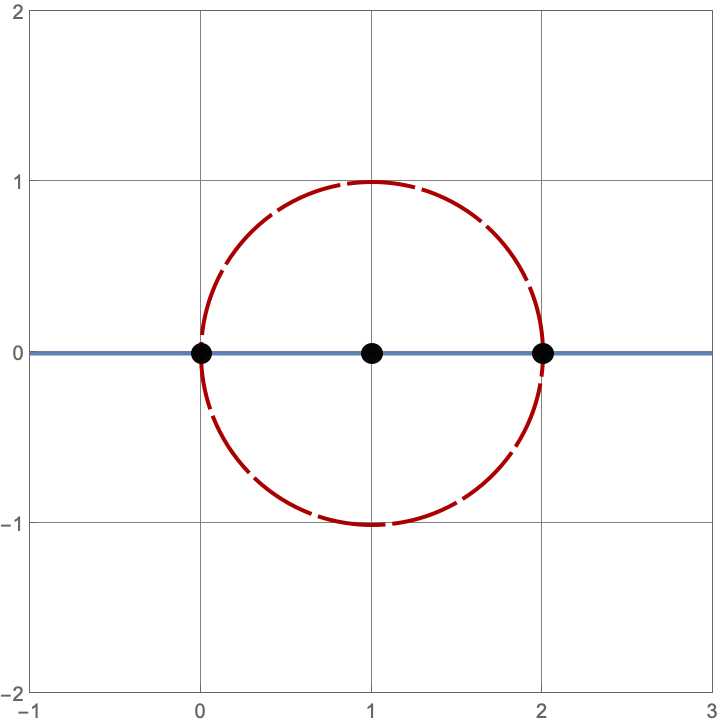
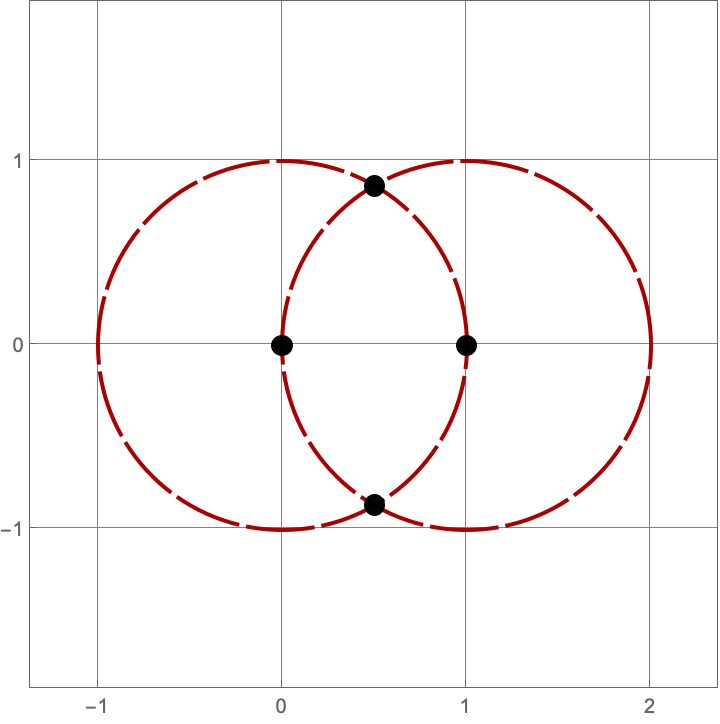
\(A383082(3) = 16\)
Here are the sixteen constructions with three lines and circles.
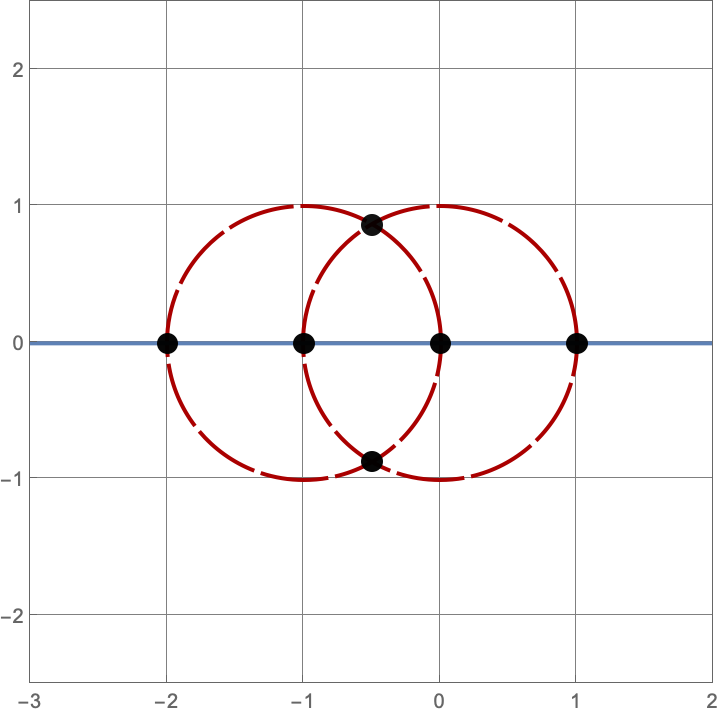
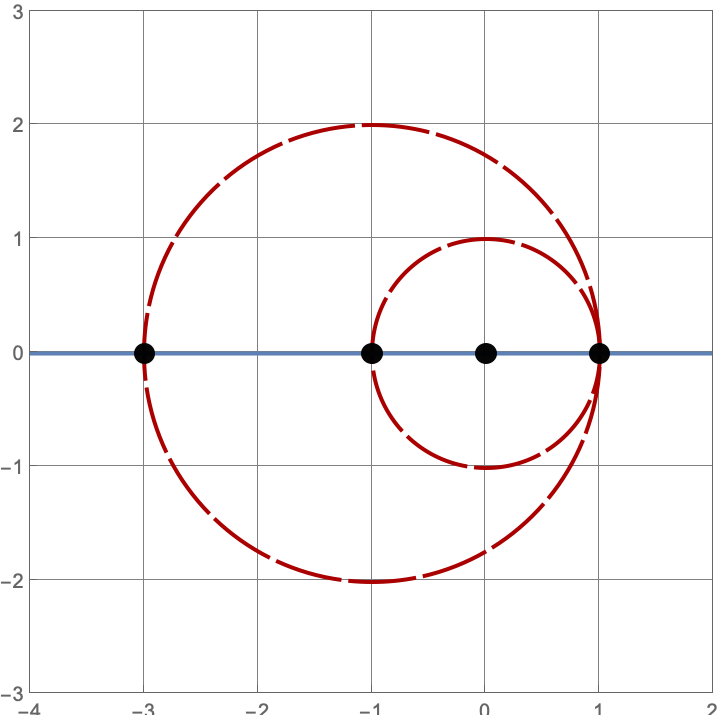
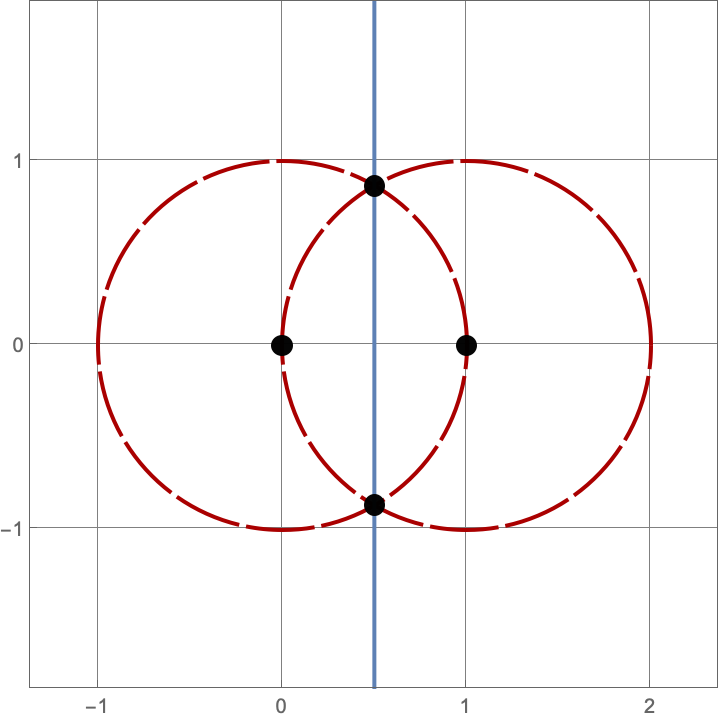
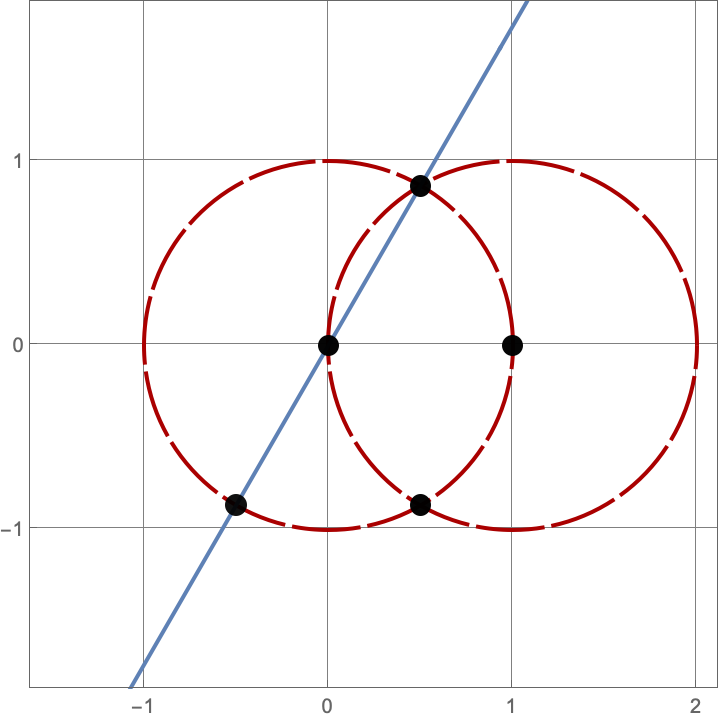
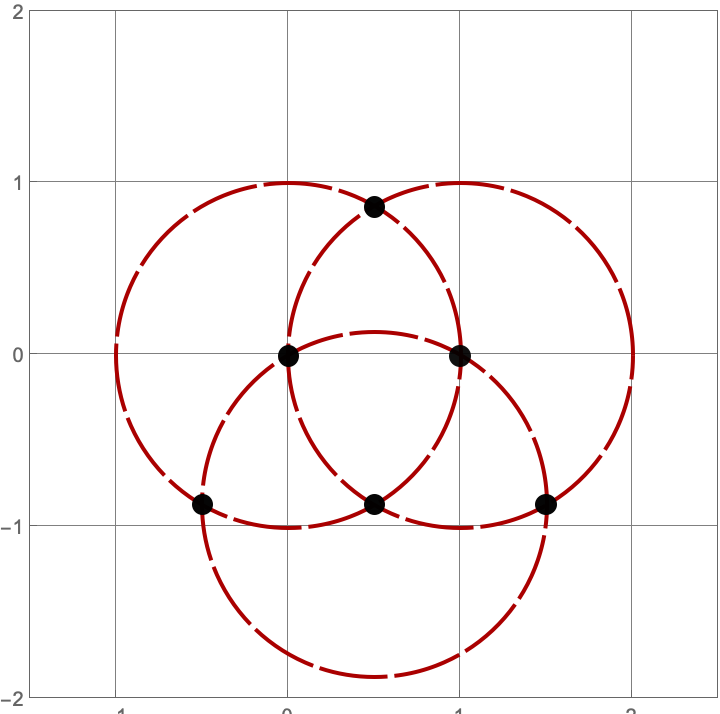
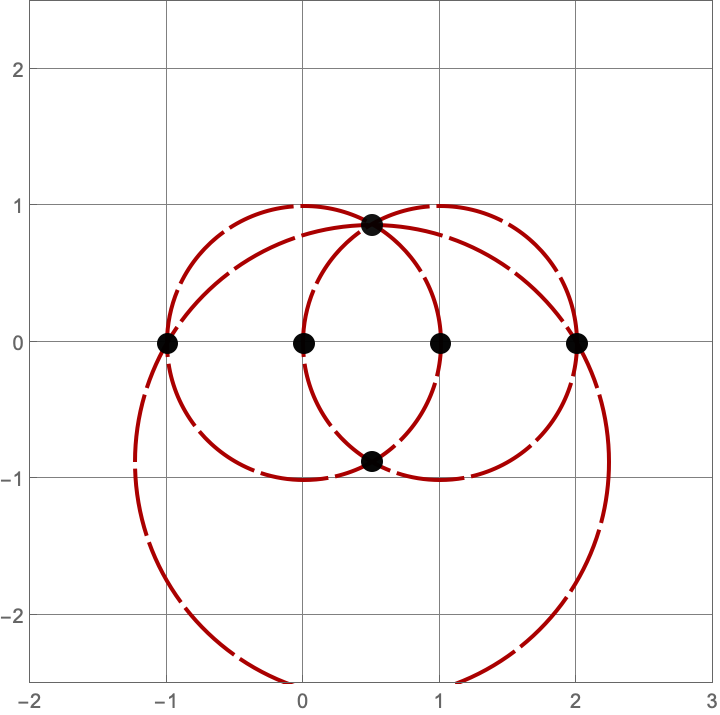
\(A383082(4) = 205\)
There are \(\operatorname{A383082}(4) = 205\) constructions with \(4\) lines and circles. Here’s a sample of five such constructions. Click on the image to see all \(205\) of them.

\(n\le5\)
Watch the video below to see all \(1 + 3 + 3 + 16 + 205 + 5886 = 6114\) constructions with \(5\) or fewer lines and circles played at 60 fps for 1.7 minutes.
Computing the sequences
In total, I computed six sequence, which I submitted to the OEIS:
- A383082: The number of distinct straightedge-and-ruler constructions that can be made with a total of \(n\) lines and circles. $$1, 3, 3, 16, 205, 5886, 542983$$
- A383083: The number of distinct straightedge-and-compass constructions that can be made with no lines and \(n\) circles.$$1, 2, 1, 4, 44, 1084, 91192$$
- A383084: The number of points in the Euclidean plane that can be determined via a straightedge-and-compass construction using \(n\) or fewer lines and circles. $$2, 2, 6, 14, 147, 5743$$
- A383085: The number of points in the Euclidean plane that can be determined via a straightedge-and-compass construction using no lines and \(n\) or fewer circles. $$2, 2, 4, 10, 52, 1704, 214135$$
- A383086: The number of distinct distances between points in the Euclidean plane where the points are constructed via a straightedge-and-compass construction using \(n\) lines and no circles. $$1, 1, 2, 4, 35, 2480$$
- A383087: The number of distinct distances between points in the Euclidean plane where the points are constructed via a straightedge-and-compass construction using \(n\) lines and circles. $$1, 1, 3, 5, 73, 6628$$
(I’m most optimistic about being able to extend A383084. I’m least optimistic about being able to extend A383083.)
Haskell code
I computed the sequence originally in Mathematica and then checked my work in Haskell using Anders Kaseorg’s library Constructible. Here’s the Haskell code that I used to compute the OEIS sequences.
module Helpers.RulerAndCompass (rulerAndCompassConstructions, compassConstructions, distinctDistances) where
import Data.Real.Constructible (Construct)
import Data.Set (Set)
import qualified Data.Set as Set
import Data.List (tails)
import Helpers.SetHelpers (flatMap)
type Diagram = (Set Point, Set Curve)
type Point = (Construct, Construct)
data Curve
= VerticalLine Construct -- x_0
| GeneralLine Construct Construct -- m & b for
| Circle Point Construct
deriving (Show, Eq, Ord)
lineFromPoints :: (Point, Point) -> Curve
lineFromPoints ((x1,y1), (x2,y2)) = if x1 == x2
then VerticalLine x1
else GeneralLine m b where
m = (y2-y1)/(x2-x1)
b = (x2*y1 - x1*y2)/(x2-x1)
dist (x1,y1) (x2,y2) = sqrt ((x2 - x1)^2 + (y2 - y1)^2)
circlesFromPoints :: (Point, Point) -> Set Curve
circlesFromPoints (p1, p2) = Set.fromList [Circle p1 r, Circle p2 r] where
r = dist p1 p2
curvesFromPoints :: (Point, Point) -> Set Curve
curvesFromPoints pts = Set.insert (lineFromPoints pts) (circlesFromPoints pts)
intersectionPoints :: Curve -> Curve -> Set Point
intersectionPoints (VerticalLine _) (VerticalLine _) = Set.empty
intersectionPoints (VerticalLine x_0) (GeneralLine m b) = Set.singleton (x_0, m*x_0 + b)
intersectionPoints (GeneralLine m b) (VerticalLine x_0) =
intersectionPoints (VerticalLine x_0) (GeneralLine m b)
intersectionPoints (GeneralLine m_1 b_1) (GeneralLine m_2 b_2) =
if m_1 == m_2 then Set.empty else Set.singleton (x_0,y_0) where
x_0 = -(b_2 - b_1)/(m_2 - m_1)
y_0 = m_1*x_0 + b_1
-- copy/pasted
intersectionPoints (Circle (x_0, y_0) r_0) (Circle (x1,y1) r1)
| d > r_0 + r1 = Set.empty
| d < abs (r_0 - r1) = Set.empty
| d == 0 && r_0 == r1 = Set.empty
| otherwise =
let a = (r_0^2 - r1^2 + d^2) / (2 * d)
h = sqrt (r_0^2 - a^2)
x2 = x_0 + a * (x1 - x_0) / d
y2 = y_0 + a * (y1 - y_0) / d
rx = -(y1 - y_0) * (h / d)
ry = (x1 - x_0) * (h / d)
in Set.fromList [(x2 + rx, y2 + ry), (x2 - rx, y2 - ry)]
where
dx = x1 - x_0
dy = y1 - y_0
d = sqrt (dx^2 + dy^2)
intersectionPoints (Circle (h, k) r) (VerticalLine x) = intersectionPoints (VerticalLine x) (Circle (h, k) r)
-- copy/pasted
intersectionPoints (VerticalLine x) (Circle (h, k) r) =
let dx = x - h
radicand = r^2 - dx^2
in if radicand < 0 then Set.empty
else
let sqrtPart = sqrt radicand
y1 = k + sqrtPart
y2 = k - sqrtPart
in if sqrtPart == 0 then Set.singleton (x, y1) else Set.fromList [(x, y1), (x, y2)]
intersectionPoints (Circle (h, k) r) (GeneralLine m b) = intersectionPoints (GeneralLine m b) (Circle (h, k) r)
-- copy/pasted
intersectionPoints (GeneralLine m b) (Circle (h, k) r) =
let a = 1 + m^2
b' = 2 * (m * (b - k) - h)
c = h^2 + (b - k)^2 - r^2
discriminant = b'^2 - 4 * a * c
in if discriminant < 0 then Set.empty
else
let sqrtD = sqrt discriminant
x1 = (-b' + sqrtD) / (2 * a)
x2 = (-b' - sqrtD) / (2 * a)
y1 = m * x1 + b
y2 = m * x2 + b
in if sqrtD == 0 then Set.singleton (x1, y1) else Set.fromList [(x1, y1), (x2, y2)]
pairs :: Set b -> [(b, b)]
pairs xSet = [ (x, y) | (x:ys) <- tails xs, y <- ys ] where
xs = Set.toList xSet
new :: ((Point, Point) -> Set Curve) -> Diagram -> Set Curve
new f (points, curves) = Set.difference allCurves curves where
allCurves = foldl Set.union curves $ map f $ pairs points
newCircles :: Diagram -> Set Curve
newCircles = new circlesFromPoints
newCurves :: Diagram -> Set Curve
newCurves = new curvesFromPoints
childDiagram :: Diagram -> Curve -> Diagram
childDiagram (points, curves) curve = (childPoints, childCurves) where
newPoints = flatMap (intersectionPoints curve) curves
childPoints = Set.union points newPoints
childCurves = Set.insert curve curves
children :: (Diagram -> Set Curve) -> Diagram -> Set Diagram
children new d = Set.map (childDiagram d) (new d)
distinctDistances :: Set Point -> Set Construct
distinctDistances ps = Set.fromList distanceList where
distanceList = [dist p1 p2 | (p1:p2s) <- tails p1s, p2 <- p2s]
p1s = Set.toList ps
initialState :: Set Diagram
initialState = Set.singleton (Set.fromList [(0,0), (0,1)], Set.empty)
compassConstructions :: [Set Diagram]
compassConstructions = iterate (flatMap $ children (new circlesFromPoints)) initialState
rulerAndCompassConstructions :: [Set Diagram]
rulerAndCompassConstructions = iterate (flatMap $ children (new curvesFromPoints)) initialState
Then we can compute A383082–A383087 with as the following:
a383082_list = map Set.size rulerAndCompassConstructions
a383083_list = map Set.size compassConstructions
a383084_list = map (Set.size . flatMap fst) rulerAndCompassConstructions
a383085_list = map (Set.size . flatMap fst) compassConstructions
a383086_list = map (Set.size . flatMap (distinctDistances . fst)) rulerAndCompassConstructions
a383087_list = map (Set.size . flatMap (distinctDistances . fst)) compassConstructions
Leave a Reply