I got nerd sniped by this first open problem described in a MathOverflow post by Richard Stanley, which suggests that there’s good reason to suspect that an innocuous-seeming combinatorial function might grows faster than any recursive function!
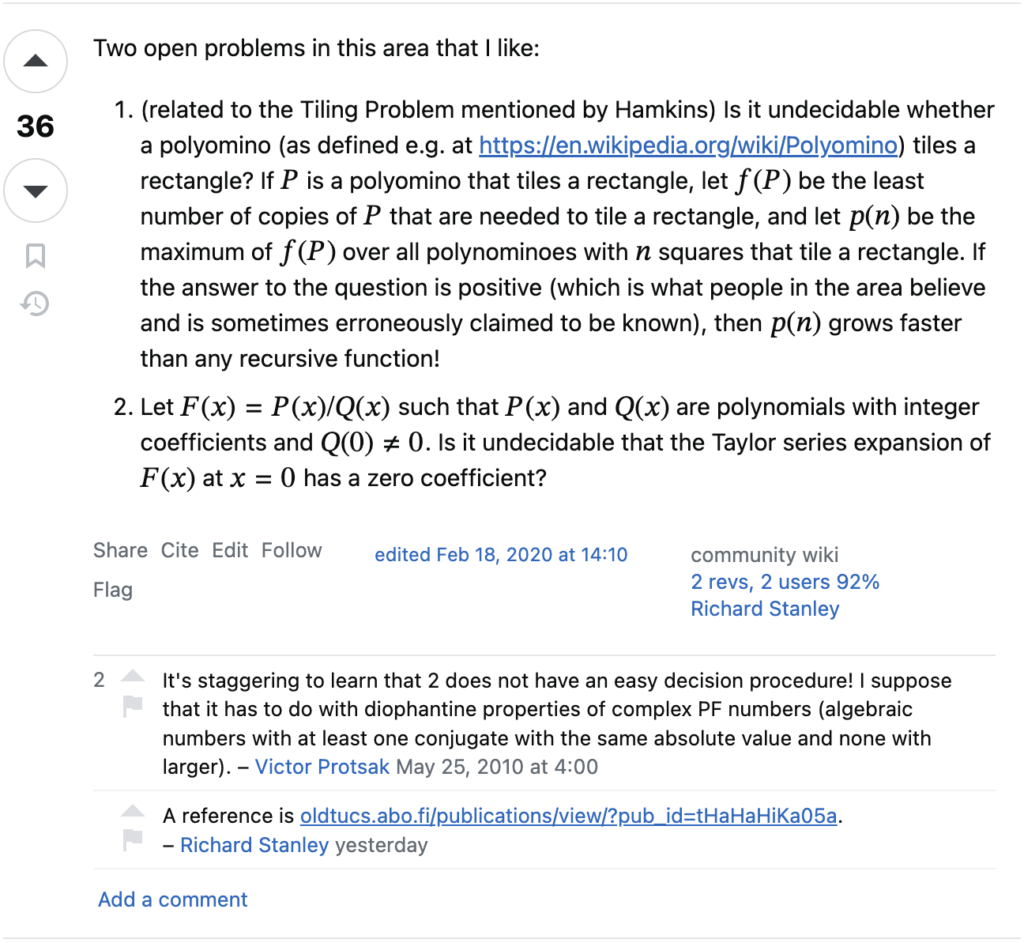
This sounds right up my alley, but I when I read this, I didn’t have any intuition for how to think about \(f(P)\) and \(p(n)\), so I wrote this post to investigate it for myself and share that with you. (After all, I tell my students: “writing is thinking.”)
My first step was to write down some examples and search for the \(p\)-sequence in the OEIS. (After all, I tell my students: “start by writing down some examples.”)
Intuition from examples
- (\(n=1\) and \(n=2\)) There’s only one \(1\)-omino, the square, and only one \(2\)-omino, the domino. Since both are rectangles, \(p(1) = p(2) = 1\).
- (\(n=3\)) There are two \(3\)-ominos:
- We can tile a rectangle with one copy of
 .
. - We can tile a rectangle with two copies of
 .
. - Therefore \(p(3) = 2\).
- We can tile a rectangle with one copy of
- (\(n=4\)) There are five free \(3\)-ominos:
- We can tile a rectangle with 1 copy of
 .
. - We can tile a rectangle with 1 copy of
 .
. - We can tile a rectangle with 2 copies of
 .
. - We can tile a rectangle with 4 copies of
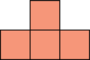 .
. - We cannot tile a rectangle with any number of copies of
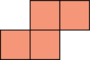 .
. - Therefore \(p(4) = 4\).
- We can tile a rectangle with 1 copy of
OEIS sequence A126140
I found OEIS sequence A126140 by searching for 1, 1, 2, 4 polyomino rectangle.

Rectifiable polyominoes
The OEIS sequence led me to Michael Reid’s website, which led me to a host of resources studying these objects. Here’s a definition of rectifiable polyominoes and their orders that matches Richard Stanley’s definition.
Archive of Recreational Mathematics: The Poly Pages
- A polyomino is said to be rectifiable if a certain number of copies of the polyomino will together form a rectangle.
- The order of a polyomino is the smallest number of pieces needed to form a rectangle.
Rectangular tilings
The following examples come from Michael Reid’s data on rectifiable polyominoes and WaybackMachine archive of Erich Friedman’s list of “Polyominoes in Rectangles.” Take a look at those links for more examples and background.
\(\operatorname{A126140}(5) = p(5) = 10\)
The largest minimal rectangle of a \(5\)-omino is a \(10\times5\) packing:
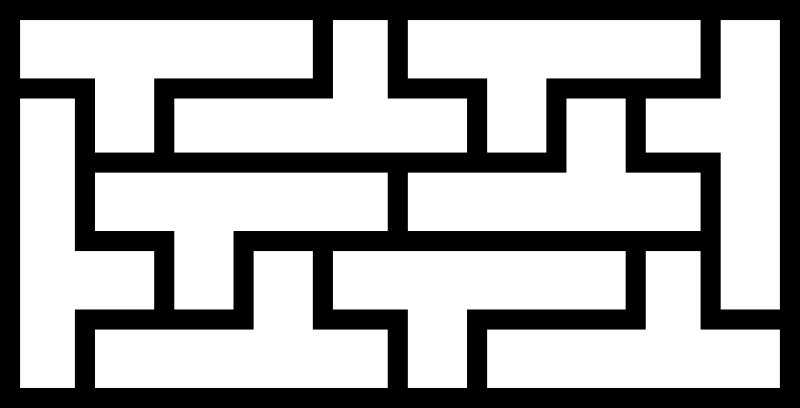
The first published example of this that I could find was by David A. Klarner in “Some results concerning polyominoes” in the Fibonacci Quarterly (1965).
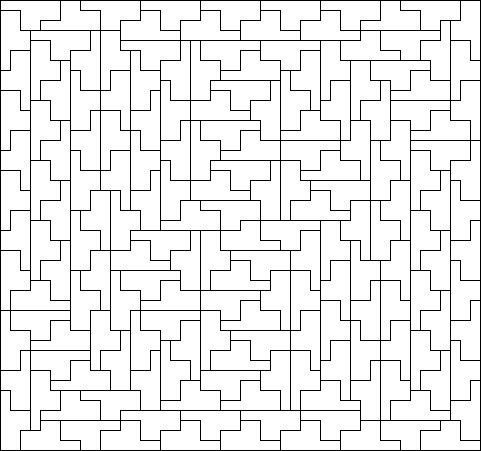
\(\operatorname{A126140}(6) = p(6) = 92\)
The largest minimal rectangle of a \(6\)-omino is a \(24\times23\) packing, which was first found by T.W. Marlow and published in Chessics #23 (1985), “the journal of generalized chess,” and then seems to have been independently discovered and published by Karl A Dahlke as “The Y-hexomino has order 92” in (the quite presigious) Journal of Combinatorial Theory, Series A.


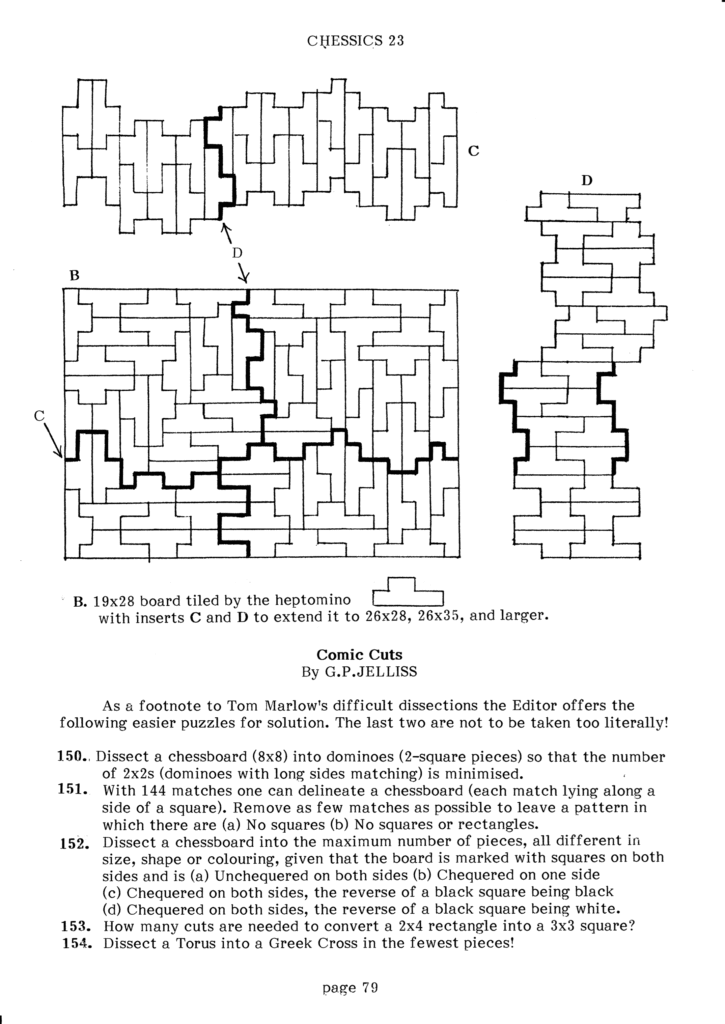
\(\operatorname{A126140}(7) = p(7)=76\)
The largest minimal rectangle of a \(7\)-omino is a \(19\times28\) packing:

This was first published by Karl A. Dahlke in JCTA in the 1989 article “A Heptomino of Order 76.”
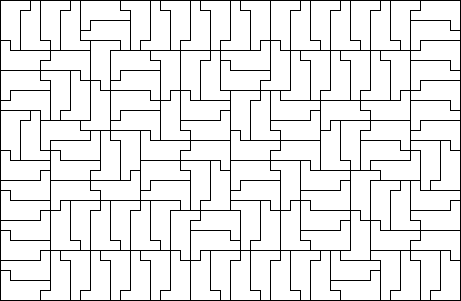
\(\operatorname{A126140}(8) = p(8)=246\)
The largest minimal rectangle of a \(8\)-omino is a \(41\times48\) packing. It looks like Karl Dahlke computes this and has the code on Github as “trec.”
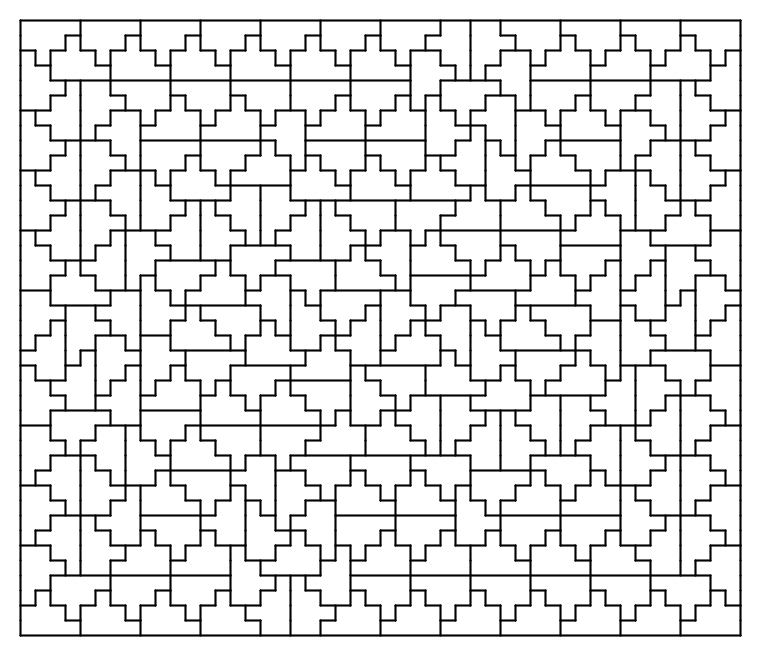
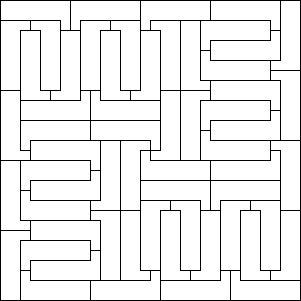
\(\operatorname{A126140}(9) = p(9)=4\)
The largest minimal rectangle of a \(9\)-omino is \(6\times6\) or \(9\times4\). Many \(9\)-ominos have \(f(P) = 4\), but the \(9\times4\) rectangle seems to occur only for one \(9\)-omino.
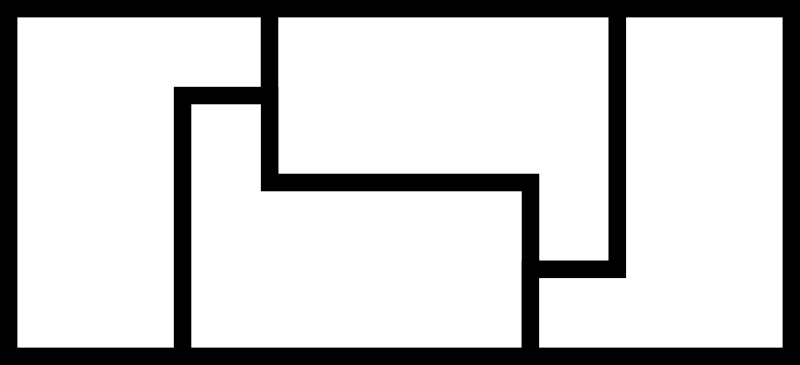
Other “prime”
Michael Reid’s data gives larger polyominos with “prime” rectangles, those which do not contain any smaller rectangle. However, it’s not clear if these rectangles are claimed to be minimal (in which case, for example, \(p(10) \geq 138\)) or if all polyominoes have been checked. Nevertheless the packings are all visually interesting, so I’ve copied them here.

Bluesky
Want to chat more about this! Let me know on Bluesky!
Leave a Reply