Hexagons in Triangles

At the beginning of April, I posted two animations related to hexagons inscribed inside of an equilateral triangle. Here I discuss a bit about the origin of these animations and give code so that you can reproduce these on your own.

Gathering 4 Gardner gift exchange

I first stumbled across this idea at the beginning of 2024 when I was making cards based on Parity Triangles for the G4G15 gift exchange: I needed to choose the size of the hexagonal arrays so that they all fit on the same triangular card, regardless of the number of rows.

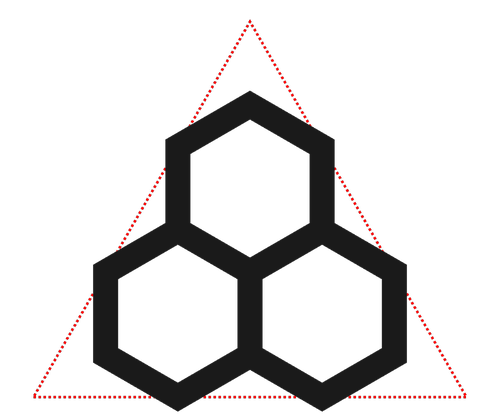
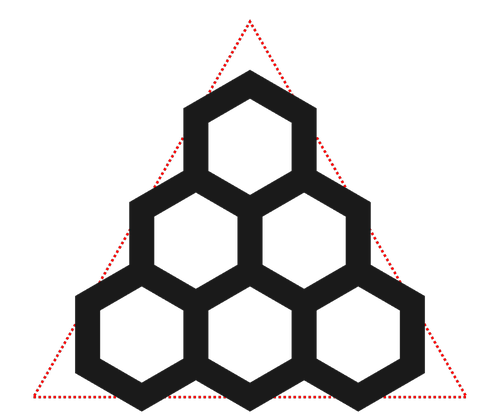
Then I started superimposing them, which created a cool effect.

Mathematica Code

The following code draws \(n\) rows of hexagons inside of the equilateral triangle with vertices \((0,0)\), \((2,0)\), and \(1, \sqrt{3}/2\).

Hexagon[{a_, b_}, n_] := Module[{x, y, r},
   r = 2/Sqrt[3] 1/(n + 1);
   x = (1 + (2 a - b)/2) Sqrt[3] r; y = r (3/2 b + 1);
   Polygon[
    Table[{x + r Cos[\[Pi]/6 (2 i + 1)], 
      y + r Sin[\[Pi]/6 (2 i + 1)]}, {i, 0, 5}]]
   ];
HexTri[n_] := 
  Flatten[Table[Hexagon[{a, b}, n], {a, 0, n - 1}, {b, 0, a}]];

First animation

The first animation opacity of the boundaries.

n = 40;
OrderIt = Reverse;
AddForms[hexTris_, t_, orderIt_] := 
 Module[{m, styleFunction, color, thickness},
  m = Length[hexTris];
  color = 
   Function[i, ColorData["Rainbow"][Mod[i*Floor[(m - 1)/2], m]/m]];
  thickness[i_] := Thickness[0.01/(1 + Sqrt[i])];
  opacity[i_] := Opacity[Median[{0, n (t - (i - 1)/n), 1}]];
  styleFunction = 
   Function[i, 
    Directive[{color[i], 
      EdgeForm[{color[i], thickness[i], opacity[i]}]}]];
  Riffle[
   styleFunction /@ orderIt[Range[m]],
   hexTris
   ]
  ]
initialStyle = {Opacity[0/100], 
   EdgeForm[{Thickness[0.0002], JoinForm["Round"]}]};
frames = Manipulate[
  Graphics[
   Join[
    initialStyle,
    AddForms[HexTri /@ OrderIt[Range[n]], 1 - Sqrt[1 - t^2], OrderIt]
    ],
   PlotRange -> {{0, 2}, {0, Sqrt[3]}},
   ImageSize -> 500],
  {{t, 1/2}, 0, 1, 1/119}
  ]

Second animation

The second video is made by increasing the thickness of the edges to fit the subsequent triangles of hexagons.

n = 20;
colors = Table[ColorData["Rainbow"][Mod[3*i, n]/n], {i, 0, n - 1}];
width = 4/3 Sqrt[3];
Interp[a_, b_] := (2 Sin[Pi/3])/
   width ((2 (-a + b))/(Sqrt[3] (1 + a) (1 + b)));
frames = Table[
   t = 1.99 + (n - 1.99)/2.001 (1 - Cos[Pi*s]);
   Graphics[
    {Opacity[0], EdgeForm[Opacity[0.5]]}~Join~
     Table[{EdgeForm[Thickness[Interp[i, t]]], EdgeForm[colors[[i]]]}~
       Join~HexTri[i], {i, 1, n}],
    PlotRange -> {{0 - ((width - 2)/2), 
       2 + ((width - 2)/2)}, {-(Sqrt[3]/3), Sqrt[3]}},
    AspectRatio -> 1,
    ImageSize -> 1080,
    Background -> Black
    ],
   {s, 0, 1 - 1/100, 1/100}
   ];